你是否想过如下问题:怎样向色盲证明两只袜子的颜色是不一样的?怎样证明两个图是不同构的?怎样证明一个数是二次非剩余的?

咋听起来觉得很有意思吧,色盲是区分不了颜色的,怎么能让他相信两只袜子的颜色不一样呢。图同构问题目前既没有被证明属于P,也没有被证明属于NP-Complete。二次非剩余问题也没有被证明属于NP。
这些听起来很“难”的问题,却可以通过交互式证明进行证明,下面先通过“向色盲证明两只袜子的颜色不同”这个有趣的例子一窥交互式证明的强大。
向色盲证明两只袜子的颜色不同
P有一只红袜子和黄袜子,她的一个色盲朋友V不相信P的袜子颜色不同,P如何才能让V相信这是真的呢?一个简单的办法如下:
- P把两只袜子给V,V每只手拿了一只袜子
- P转过身背对V
- V抛一枚硬币,如果头面朝上,则保持两只袜子不动,否则交换左右手的袜子
- P转过身,V问P是否交换过袜子
- 如果P回答错误,则V不相信;否则,重复100次实验,如果P都回答正确,则V相信这两只袜子是不同颜色的
如果两只袜子的颜色确实不一样,则P通过区分两只袜子的颜色能正确回答V有没有交换过袜子。但是如果两只袜子颜色一样,则不管V有没有交换过,P都无法分辨这两只袜子,所以只好猜V有没有交换,而猜对的概率只有1/2,重复100次,都猜对的概率只有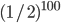 ,这是一个非常小的数,可以认为几乎不会发生,即出错的概率极低。
,这是一个非常小的数,可以认为几乎不会发生,即出错的概率极低。
这就是交互式证明的一个例子,上述证明有三个特点:1)交互过程,整个证明需要P和V进行交互才能完成;2)具有随机性,即V需要抛一枚硬币,来决定是否交换袜子;3)零知识,虽然V最终相信了这两只袜子是不同颜色的,但V还是不知道这两只袜子是什么颜色的。
下面我们给出交互式证明的形式化定义。
交互式证明(Interactive Proofs, IP)
令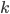 是
是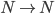 的一个函数,我们称语言
的一个函数,我们称语言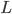 属于
属于![IP[k]](http://bitjoy.net/wp-content/plugins/latex/cache/tex_8ee6b800dc5dcde66343bf178eab2e8d.gif) ,如果存在一个
,如果存在一个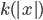 多项式时间概率图灵机TM
多项式时间概率图灵机TM 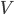 ,使得:
,使得:
![x\in L \Longrightarrow\exists P\quad Pr[V \text{ accepts }x, V(x)=1]\geq 2/3\\ x\notin L \Longrightarrow\forall P\quad Pr[V \text{ accepts }x, V(x)=1]\leq 1/3](http://bitjoy.net/wp-content/plugins/latex/cache/tex_90516f6df3d914be79f4f7f6745bca8f.gif)
定义
![IP=\underset{c}{\bigcup} IP[n^c]](http://bitjoy.net/wp-content/plugins/latex/cache/tex_a7a6a8fb25e603d35f739211c4ee5dee.gif)
上述定义的第一条称为“完备性”(Completeness):如果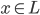 ,则存在一个证明者P(prover),使得验证者V(verfier)能以多项式时间接受
,则存在一个证明者P(prover),使得验证者V(verfier)能以多项式时间接受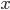 ,且接受的概率大于2/3;第二条称为“可靠性”(Soundness),如果
,且接受的概率大于2/3;第二条称为“可靠性”(Soundness),如果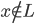 ,则对于所有证明者P,V接受
,则对于所有证明者P,V接受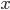 的概率都不会超过1/3。
的概率都不会超过1/3。
对应到上面的例子,完备性:当两只袜子的颜色确实不同时,V接受的概率为1>2/3;可靠性:当两只袜子的颜色相同时,重复100次实验,V接受的概率只有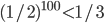 。
。
IP这个复杂性类就是所有IP[k]的并集。在IP中,P的能力是无穷的,但它不一定是诚实的;V能力较弱,只能进行多项式时间的计算。
下面我们给出另外两个交互式证明的协议。
图不同构(Graph Non-isomorphism, GNI)的交互式证明
如果图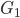 和
和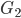 可以通过对顶点进行恰当标记来将它们转换为同一个图,则称
可以通过对顶点进行恰当标记来将它们转换为同一个图,则称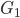 和
和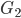 同构,记为
同构,记为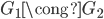 。换句话说,如果
。换句话说,如果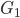 和
和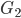 同构,则在
同构,则在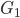 的所有顶点标签上存在一个置换
的所有顶点标签上存在一个置换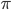 使得
使得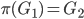 ,其中
,其中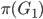 是将
是将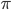 作用到
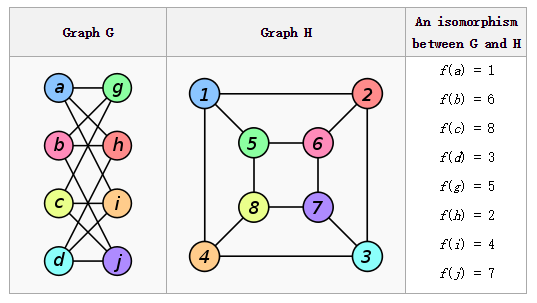
作用到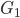 的各个顶点上之后得到的图。下图就是两个同构图,右边给出了置换
的各个顶点上之后得到的图。下图就是两个同构图,右边给出了置换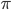 。
。
图同构的补集为图不同构(Graph Non-isomorphism, GNI),即判定给定的两个图是否不同构。下面是GNI的一个交互式证明过程。
给定两个图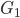 和
和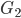 ,证明者P想要向验证者V证明
,证明者P想要向验证者V证明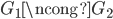 。
。
- V:随机选一个
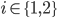 ,对
,对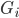 做一个随机的置换,得到新图
做一个随机的置换,得到新图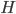 ,则有
,则有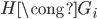 ,将
,将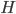 发送给P
发送给P - P:发送
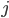 给V
给V - V:如果
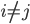 ,则拒绝;否则重复100次实验,都有
,则拒绝;否则重复100次实验,都有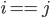 ,则相信
,则相信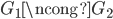
完备性:如果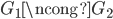 ,则
,则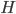 只和
只和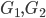 中的一个图同构,P因为能力无穷,一定能找出和
中的一个图同构,P因为能力无穷,一定能找出和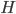 同构的图
同构的图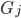 ,且满足
,且满足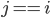 。
。
可靠性:如果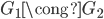 ,则
,则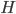 和
和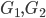 都同构,所以P无法区分,只好猜一个
都同构,所以P无法区分,只好猜一个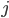 ,所以
,所以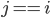 的概率只有1/2,重复100次实验,P都猜对的概率只有
的概率只有1/2,重复100次实验,P都猜对的概率只有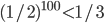 。
。
零知识:虽然V相信了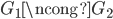 ,但V对于P怎样证出来的一无所知。
,但V对于P怎样证出来的一无所知。
P.S.
有趣的是,关于图同构问题,芝加哥大学的科学家László Babai最近给出了一个伪多项式时间的算法,被称为是计算机理论界近10年最重要的成果。
- New algorithm cracks graph problem
- A Quasipolynomial Time Algorithm for Graph Isomorphism: The Details
- Graph Isomorphism in Quasipolynomial Time
- 图同构在P/NP问题上重大突破,计算机理论10年最重要成果
二次非剩余(Quadratic non-residuosity, QNR)的交互式证明
如果存在整数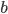 使得
使得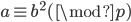 ,则称整数
,则称整数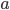 是模
是模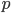 的二次剩余,并称
的二次剩余,并称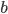 是
是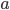 模
模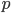 的平方根。显然,
的平方根。显然,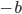 是
是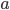 模
模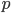 的另一个平方根,而且
的另一个平方根,而且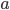 模
模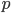 不存在其他平方根,因为
不存在其他平方根,因为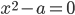 在域
在域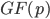 上至多有两个解。
上至多有两个解。
类似的,如果不存在整数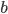 使得
使得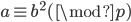 ,则称整数
,则称整数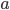 是模
是模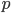 的二次非剩余(Quadratic non-residuosity, QNR),记为
的二次非剩余(Quadratic non-residuosity, QNR),记为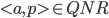 。下面是QNR的一个交互式证明过程。
。下面是QNR的一个交互式证明过程。
给定一个素数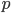 和另一个整数
和另一个整数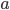 ,P要向V证明
,P要向V证明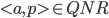 。
。
- V:取模
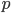 的随机数
的随机数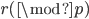 和随机数
和随机数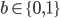 ,如果
,如果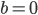 ,发送
,发送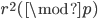 给P;否则发送
给P;否则发送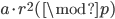 给P
给P - P:发送
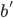 给V
给V - V:如果
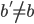 ,则拒绝;否则重复100次实验,都有
,则拒绝;否则重复100次实验,都有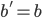 ,则相信
,则相信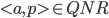
完备性:如果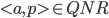 ,则
,则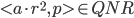 但
但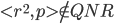 ,所以P能区分
,所以P能区分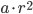 和
和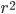 ,即总能回答正确使得
,即总能回答正确使得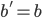 。
。
可靠性: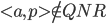 ,则
,则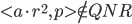 且
且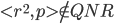 ,即
,即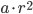 和
和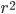 都是二次剩余,所以P无法区分,只能瞎猜,正确的概率为1/2,重复100次,都回答正确的概率只有
都是二次剩余,所以P无法区分,只能瞎猜,正确的概率为1/2,重复100次,都回答正确的概率只有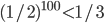 。
。
零知识:虽然V相信了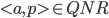 ,但V对于P怎样证出来的一无所知。
,但V对于P怎样证出来的一无所知。
交互式证明的零知识真是有趣,它是密码学中大量研究工作的基础。很多场合都可能会用到零知识证明,比如要向别人证明你有密码,但又不透露密码;要向别人证明你会解某道题,但又不透露解题过程;要让别人相信你知道怎样从甲地到乙地,但又不告诉别人从甲到乙的路......
交互式证明是这学期选修《高级算法》时接触的,主要参考书目Computational Complexity: A Modern Approach
为什么交互式证明正确的概率不是1 而是大于三分之二
“如果∈QNR,则∈QNR但∉QNR”没懂,按这个定义,r^2不应该天然属于二次剩余吗,令r^2=a,r=b,这样就满足公式了,r^2就是二次剩余了