今天我们终于进入到了本书的重头戏——深度学习。其实,这一章的深度学习主要介绍的是卷积神经网络,即CNN。
本书之前的章节介绍的都是如下图的全连接网络,虽然全连接网络已经能够在MNIST数据集上取得98%以上的测试准确率,但有两个比较大的缺点:1. 训练参数太多,容易过拟合;2. 难以捕捉图片的局部信息。第一点很好理解,参数一多,网络就难以训练,难以加深。对于第二点,因为全连接的每个神经元都和上一层的所有神经元相连,无论距离远近,也就是说网络不会捕捉图片的局部信息和空间结构信息。

本章要介绍的卷积神经网络,相对于全连接网络,有如下三个特点:1. 局部感知local receptive fields 2. 权值共享shared weights 3. 池化pooling,下面分别介绍这三部分内容。
局部感知
对于MNIST的一张28*28灰度图片,全连接网络的输入把图片展开成一个维度为784的向量,这就天然丢失了图片的空间结构信息。而CNN的输入保持了图片28*28的二维空间结构信息,相应的,CNN的中间层也是二维的。这就涉及到输入层的二维图片和隐藏层的二维图片如何对应的问题。
CNN使用一个被称为“卷积核”的东西,把输入图片转换为隐藏层的特征图(feature map),如下图所示,假设卷积核大小为5*5,则输入图片每5*5的一个小区域被转换为隐藏层的一个神经元(像素),这个小区域就称为局部感受野。

当卷积核不断的在输入图片中移动时,假设每次移动一格(stride=1),则原来28*28的图片,经过一次卷积后,得到的feature map大小为24*24,相比输入图片小了一圈。

权值共享
那么,这个卷积操作具体是怎样执行的呢,非常简单。5*5的卷积核本质是一个5*5的矩阵,矩阵中的每个值相当于这个卷积核的参数,或者说权值w。每次卷积时,5*5的矩阵和输入图片中5*5的感受野对应位相乘再相加得到隐藏层的一个值。
下图是一个缩小版的动图例子,左图的绿色大图相当于输入的5*5图片,移动的黄色小图相当于当前卷积的感受野,大小为3*3。在这个3*3的感受野中,每个单元格居中的数字是输入图片的像素值,右下角的红色小字表示卷积核的权值。每次卷积操作,感受野内的图片像素和卷积核权值相乘再相加,得到右图红色小图中的一个单元格的值,这就完成了一次卷积。当黄色感受野不断在输入图片中移动时,右边的feature map也不断被填充,直到一轮卷积完成。整个过程进行了9次卷积,feature map的大小为3*3=9卷积次数。
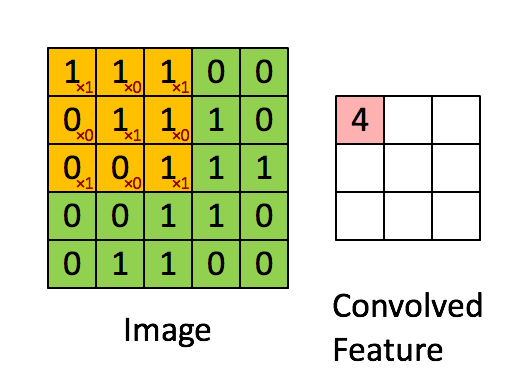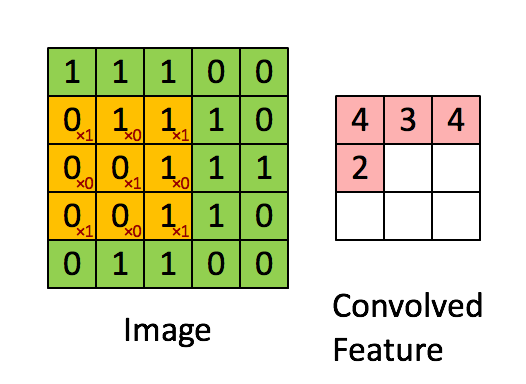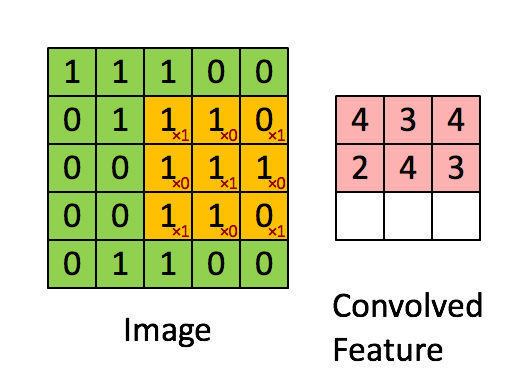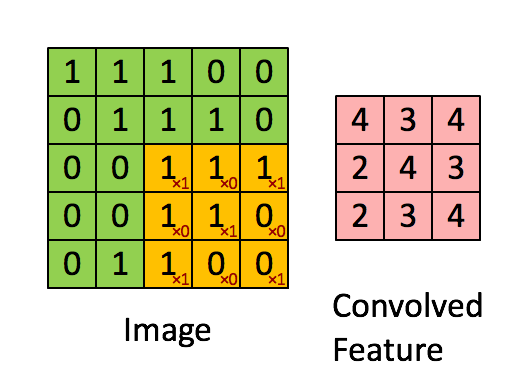
这里又涉及到CNN的第二个特点——权值共享。注意到,对于上图的一轮卷积操作,不同感受野内右下角的权值矩阵是一样的,也就是说9次卷积的卷积核权值是一样的。权值共享有两个好处,一是特征位置无关,二是参数量大大下降。
对于特征位置无关 。这个3*3的卷积核相当于一个特征提取器或者说滤波器,比如这个特征提取器能够提取“猫”这个特征,则无论猫在输入图片的左上角还是右下角,“猫”这个特征都能被提取出来,因为卷积核在小范围移动,无论“猫”位于图片的哪个区域,当卷积核移动到这个区域时,卷积得到的输出比较大,被激活,得到“猫”这个特征。所以CNN对位置不敏感,这对图像处理尤其有利。正因为这个特点,经过卷积核卷积操作之后的小图片(上图右边的红色图片)被称为特征图(feature map),因为它就是用卷积核提取出来的符合这个卷积核描述的一个特征。
对于参数量大大下降。事实上,一次卷积操作除了上面动图显示的卷积核与感受野内的图片相乘再相加之外,还会对加和之后的值做一个激活输出。回到我们的MNIST例子,一次卷积操作用公式来表示就是:
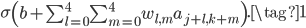
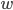 表示卷积核权值矩阵,
表示卷积核权值矩阵,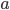 表示感受野内的输入图片,两个累加
表示感受野内的输入图片,两个累加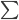 就是上面动图显示的相乘相加过程,得到和之后,还会加上一个偏移量
就是上面动图显示的相乘相加过程,得到和之后,还会加上一个偏移量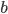 ,最后进行激活输出
,最后进行激活输出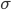 。所以一个5*5的卷积核,参数量为5*5+1=26。如果有20个卷积核,参数总量为20*26=520。但如果是全连接网络,假设隐藏层有30个,则参数量为784*30+30=23550。所以仅考虑隐藏层的参数量,CNN就比全连接网络少了45倍的参数,参数量少了,就能加快训练,网页也有可能加深。
。所以一个5*5的卷积核,参数量为5*5+1=26。如果有20个卷积核,参数总量为20*26=520。但如果是全连接网络,假设隐藏层有30个,则参数量为784*30+30=23550。所以仅考虑隐藏层的参数量,CNN就比全连接网络少了45倍的参数,参数量少了,就能加快训练,网页也有可能加深。
池化
池化就很好理解了,对于卷积得到的feature map,再画一个框(类似于卷积层的感受野),把框内的最大值取出来作为池化之后的值,这就是max-pooling。池化的目的是用来简化信息的,相当于降维。池化的框也可以称为核kernel,如果kernel的大小是2*2的,则一个24*24的feature map,经过max-pooling之后就变成了12*12了,维度瞬间降了一半, 把原来的feature map变成了一个紧凑的feature map。

池化层往往跟在卷积层的后面,下图表示一张28*28的图片,使用3个5*5的卷积核之后,得到了3个24*24的feature map,再经过2*2的max-pooling,得到3个12*12的feature map。

到这里,CNN的三大特点就介绍完毕了。对于上图,三个卷积核相当于提取了三种特征,我们还需要完成最终的分类任务,这时候还得把全连接网络请过来。经过max-pooling之后,我们再接一个包含10个神经元的全连接层,作为输出层,完整的网络结果如下:

最后的全连接层和我们前面介绍的全连接网络是完全一样的,只不过全连接的输入是3个经过max-pooling之后的feature map,在和输出层相连时,可以想象成先把3个12*12的feature map展开并首尾相连,得到一个3*12*12=432的向量,再和输出层的10个神经元进行全连接。这就是一个非常简单的CNN网络,包含一个输入层、一个卷积层、一个池化层和一个输出层。
本文的代码示例network3.py中,构建了一个和上图类似的简单的CNN网络,如下图所示,使用了20个卷积核,相当于提取了20种特征;max-pooling之后使用了两个全连接层,前一层包含100个隐藏神经元,使用sigmoid激活;后一层包含10个神经元,使用softmax激活,作为输出层。就是这么一个简单的CNN网络,其在测试集上的准确率达到了98.78%,超过了本文之前构建的所有的全连接网络。

由于原文使用的是已经不再维护的Theano,本博客不打算详细介绍其代码实现,我将在稍后的博文中分享Pytorch的CNN代码。不过我还是把原文对CNN的优化过程总结如下,用测试集的准确率作为性能指标:
- 上图简单的CNN网络,98.78%
- 增加一个卷积层,且把激活函数换成ReLU,99.23%
- 数据增强,把原有的5000张图片,上下左右各平移一个像素,增加了4倍数据,99.37%
- 增加一个全连接层,且全连接层神经元增加为1000个,使用dropout=0.5,epoch相应减少到40个,99.6%。因为卷积层有权值共享,天然参数少防止过拟合,所以dropout一般只用于全连接层
- 模型融合ensemble,5个上述模型,采用majority vote,99.67%,已接近人类水平
虽然经过上述5步,准确率没有达到100%,但那些分类错误的图片,真的很难说分错了,因为图片看起来就不是它标注的结果(右上角),就应该是分错的结果(右下角)。总的来说,我觉得已经非常不错了。

稍微解释两个问题。
一、为什么ReLU比Sigmoid性能好,目前还没有一个令人信服的答案,只是很多人在很多标准数据集上测试,发现ReLU性能比Sigmoid好,这个消息传开之后,大家都开始用ReLU了。通常的解释是ReLU的max(0,z)在z很大时,梯度依然为1,不存在梯度消失的问题;而Sigmoid在z很大时,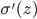 梯度几乎为0,存在梯度消失的问题。
梯度几乎为0,存在梯度消失的问题。
二、为什么CNN可以做深?怎样解决上一章提到的梯度消失或者梯度爆炸问?事实上,CNN并没有解决上一章的问题,而是绕过了这个问题:1) 卷积层大大减少了模型参数,使得网络更加简单,可以训练得更快;2)强大的正则减少过拟合:dropout和卷积层;3)使用ReLU而不是sigmoid,可以加速训练过程3~5倍;4)使用GPU,并且愿意训练更长的时间,因为sigmoid的梯度消失只不过是梯度很小更新很慢,如果训练时间足够长的话,应该也能收敛。而如果用GPU的话,训练速度加快了,相同时间就可以训练更多的epoch。组合3和4,相当于比之前的网络训练时长增加了30倍,收敛效果自然会更好。
除了CNN,文章最后还简单提到了图像识别的进展、深度学习的其他应用以及神经网络的未来等内容,本博客就不想洗介绍了,有兴趣的可以去看原文。
附录:LeNet-5和多通道卷积
这部分内容是我自己加的,书中提到network3.py是模仿著名的LeNet-5,我于是就查了查LeNet-5的文章和相关介绍。

上图就是非常经典的LeNet-5网络结构图,包含2个卷积层、2个池化层、2个全连接层和1个Gaussian connections。目前比较流行的做法中已经把最后一个Gaussian connections换成了全连接层。本博客前面介绍的卷积层输入只有一张图片,比较好理解,但是LeNet-5的C3即第二个卷积层,面对的是S2得到的6张feature map,相当于有6张输入图片,如何做卷积。
这就涉及到“多通道”卷积的概念,可以把多通道理解为S2的6个feature map之于C3,一个feature map理解为一个通道。事实上,如果输入图片是彩色的,则输入图片就包含R、G、B三个通道,相当于输入了3张feature map,此时在C1中就会遇到“多通道”卷积的问题。
假设输入有R、G、B三个通道,则每个通道都需要有一个不同的卷积核进行卷积,最后把三个通道的卷积结果加起来,进行激活,如下面动图所示。
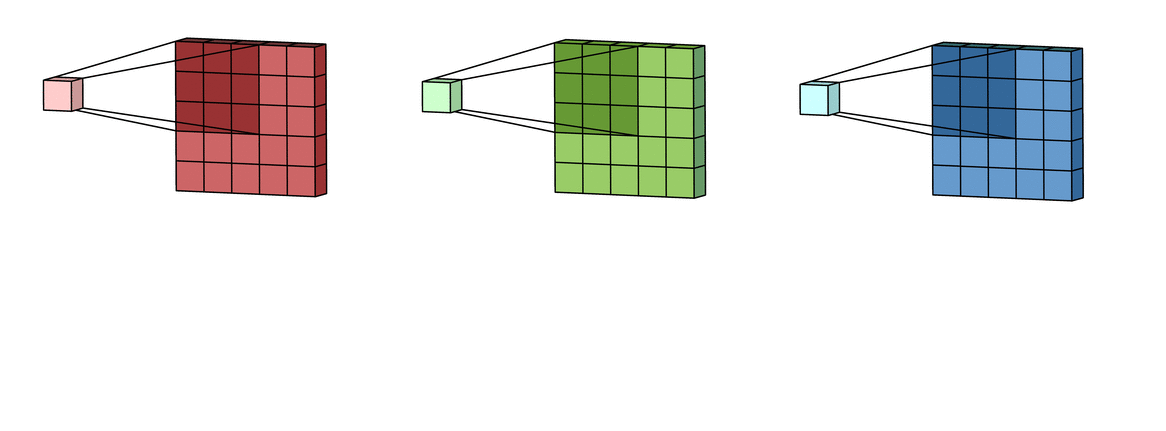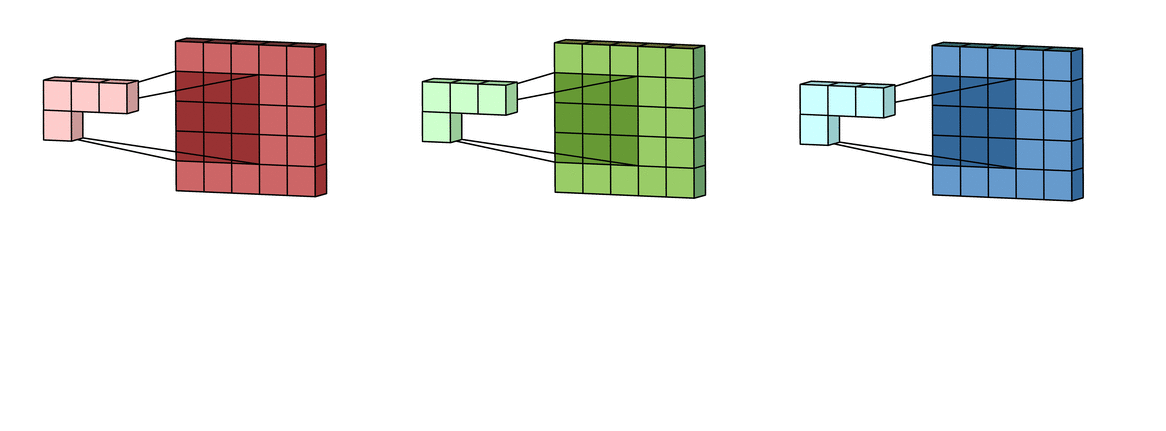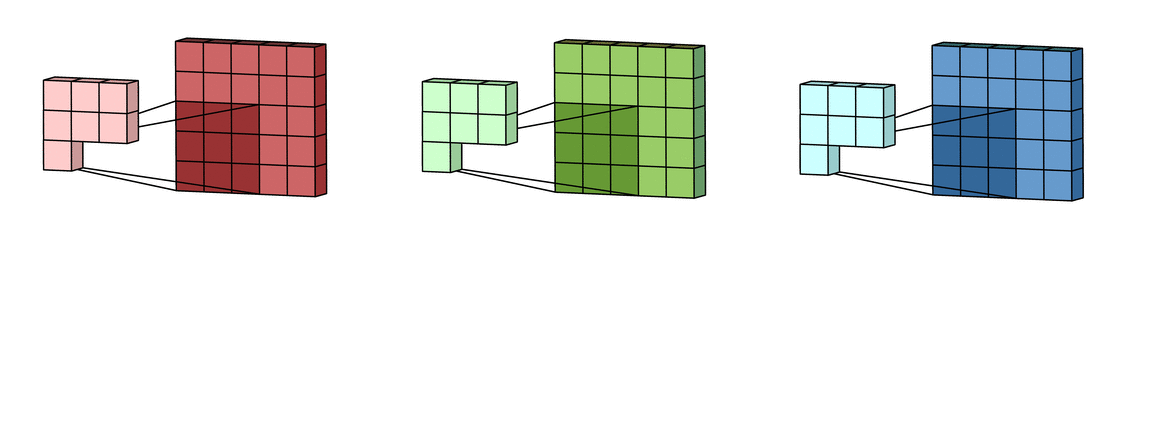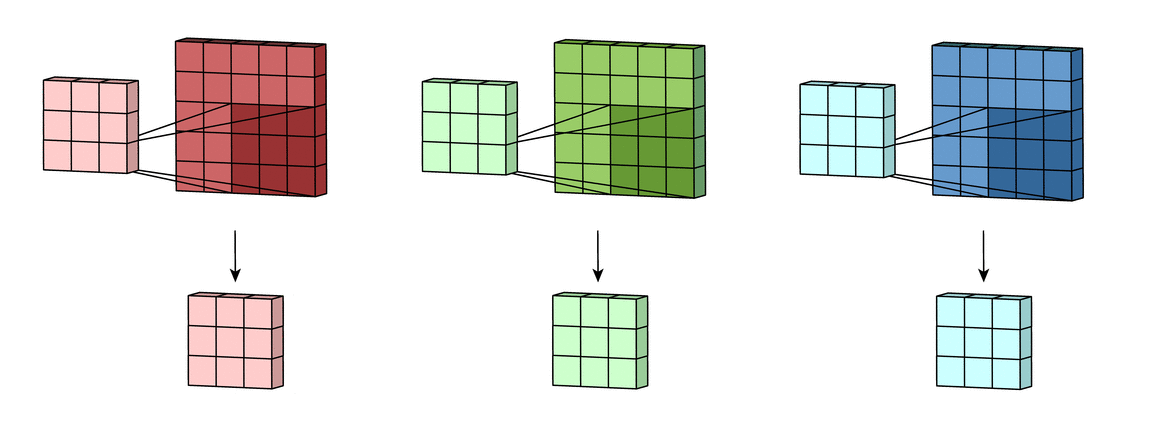
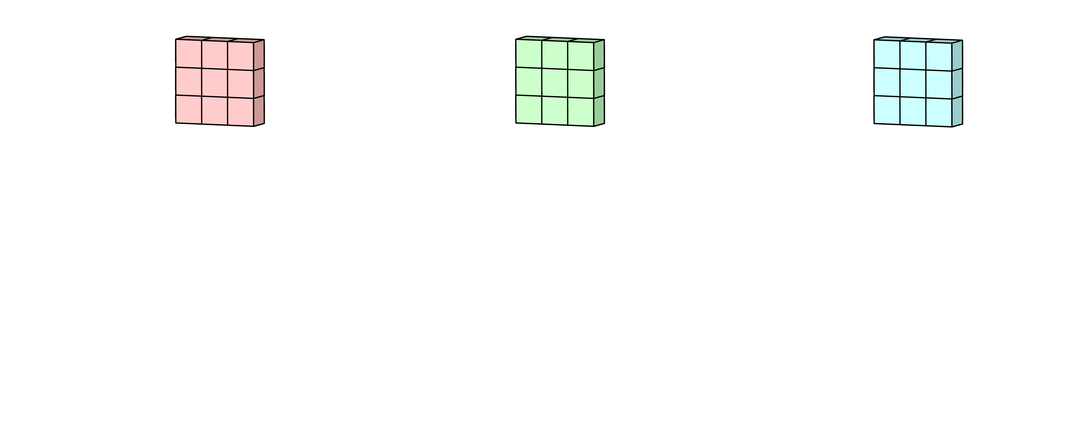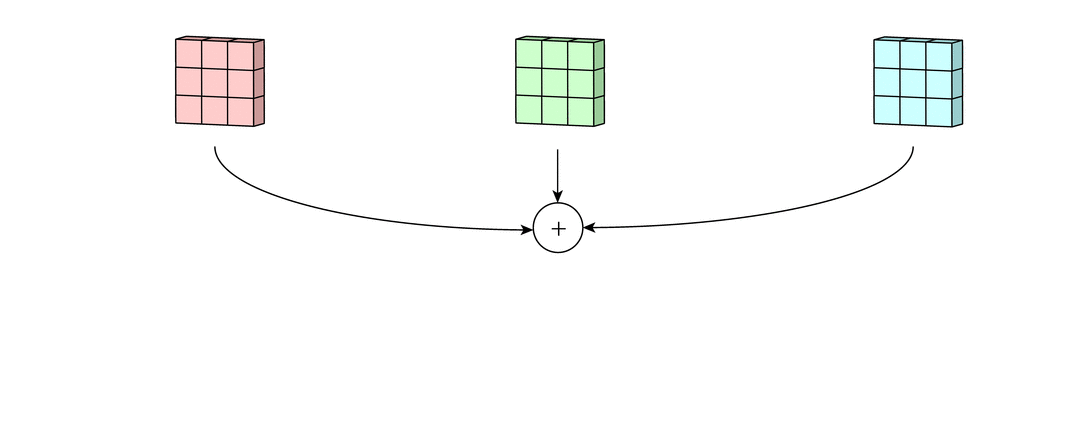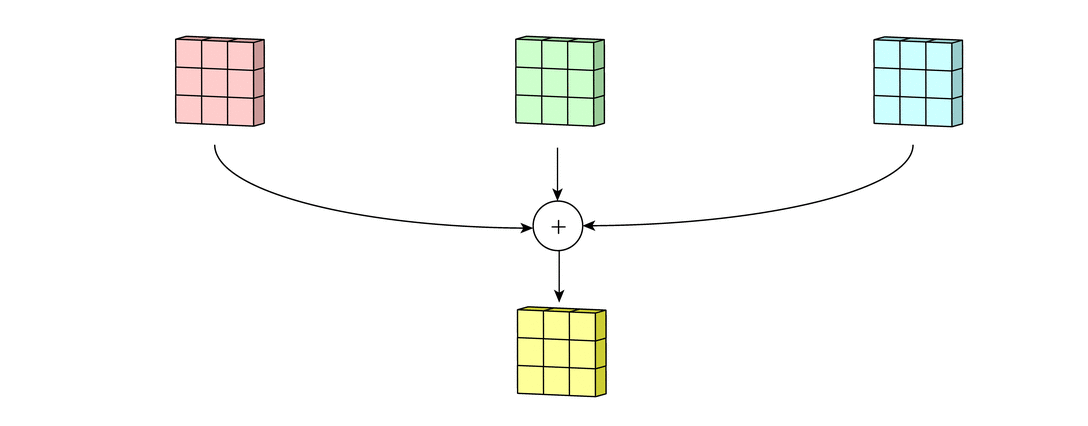
回到LeNet-5,S2有6个通道,C3得到了16个feature map,说明C3有16个卷积核。但是,C3每个卷积核并不只包含一个卷积矩阵,而是包含三个卷积矩阵,即每个卷积核也是三通道的,而且这三个通道的卷积矩阵参数是不同的,即不共享,它们只共享一个偏移量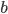 ,如下图所示。
,如下图所示。

但是S2有6个feature map,三个通道不够用,所以LeNet-5的论文中还规定了每个卷积核的三通道卷积S2中的哪3个feature map,如下图所示。

如果还不理解的话,CS231N还有一个更直观的例子:
https://cs231n.github.io/assets/conv-demo/index.html 可以点击按钮暂停,然后手动计算看看是否和动图的结果一致。

有关CNN和LeNet-5的参考资料:
- CNN直观解释:
https://www.zhihu.com/question/39022858/answer/224446917 - 可视化卷积:
https://hackernoon.com/visualizing-parts-of-convolutional-neural-networks-using-keras-and-cats-5cc01b214e59 - 可视化“多通道”卷积:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1 - 动图展示“多通道”卷积:
https://cs231n.github.io/convolutional-networks/ - LeNet-5原文:
http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf - LeNet-5网络解读:https://blog.csdn.net/saw009/article/details/80590245
Pingback: CS224N(2.12)Convolutional Networks for NLP | bitJoy