进入研究生生涯完成的第一个新生培训作业是“2.5亿个浮点数的外部排序算法”，前后折腾了将近一个月，结果是在i7处理器上，限制512MB内存，排序用时250秒左右。

这个作业的常规思路大部分人都能想到，按块读取文件->atof转换为double->内部快速排序或基数排序->dtoa转换为char*->按块写入文件。这里面中间的三个过程都很耗时，特别是atof和dtoa，因为精度只要求保留9位小数，所以可以自己实现atof和dtoa来加速，也可以使用多线程加速。

整个作业都是基于对IEEE754浮点数的深刻理解展开的，所以下面详细讲解浮点数的一些知识。

IEEE754双精度浮点数

目前大多数CPU内浮点数的表示都遵循IEEE754标准，IEEE754双精度浮点数（double）表示如下图所示。

sign bit：符号位，1位，用来表示正负号，0表示非负；1表示负

exponent：指数位，11位，用来表示次方数，是一个无符号数

fraction：尾数位，52位，用来表示精确度，也是一个无符号数，有些资料也叫做mantissa或significand

这种表示形式有两点需要注意。

第一，既然exponent是无符号的，那么怎样表示负指数呢？

IEEE754规定，二进制串中算得的e需要减去一个偏移量bias，对于double，bias=1023，即e'=e-bias。因为$e\in[0,2^{11}-1]$，所以最终$e'\in[-2^{10}+1,2^{10}]$。但是如果把e本身看作有符号数e''，则$e''\in[-2^{10},2^{10}-1]$，既然e''和e'相差微小，为什么不直接把e看成有符号数，而非要把它看成无符号数，再减去一个偏移量bias呢？

这是因为如果把e看成无符号数再减偏移量，浮点数大小比较速度更快。引用维基百科的一段话：

By arranging the fields so that the sign bit is in the most significant bit position, the biased exponent in the middle, then the mantissa in the least significant bits, the resulting value will be ordered properly, whether it's interpreted as a floating point or integer value. This allows high speed comparisons of floating point numbers using fixed point hardware.

对于两个正浮点数a和b，如果a>b，则a的二进制字符串的字典序也相应的在b的后面；对于负数则正好相反。也就是说，无论是把这个数看成浮点数还是整数，都可以通过只比较两个数的二进制串得出大小关系，而不需要通过公式计算其十进制值再比较大小，这显然加快了比较速度。

浮点数的这个特性使得对浮点数排序也可以使用基数排序！很神奇吧，具体是这样的：先对二进制串进行分组，按先低位组后高位组对其进行基数排序；当到最高位组时，把负数放到正数的前面逆序排列，正数常规排列，得到的就是有序的排列。

比如，假设把数看成无符号数时，会得到下面的基数排序结果，此时需要调整顺序，把正数统一移到后面，就是代码第50行：index += negatives；把负数移到前面的同时逆序排列，相当于在0的上面画一条线，然后-1,-2,-7以这条线做一个翻折对称，所以新的负数的下标变成了第48行的：index = n - index - 1。

　0　　:　　0000
　1　　:　　0001
　2　　:　　0010
　4　　:　　0100
　-1　 :　　1001
　-2　 :　　1010
　-7　 :　　1111　　

变成：

　-7　 :　　1111　　
　-2　 :　　1010
　-1　 :　　1001
　0　　:　　0000
　1　　:　　0001
　2　　:　　0010
　4　　:　　0100

具体的实现可以看这个讨论，下面是我实现的C++版本。

void RadixSort(std::vector<double> &nums) {
    int n = nums.size();
    vector<LL> t(n), a(n);
 
    for (int i = 0; i < n; i++)
        a[i] = *(LL*)(&nums[i]); //将double的二进制转换为long long
 
    int groupLength = 16; //可自定义
    int bitLength = 64;
    int len = 1 << groupLength;
 
    vector<int> count(len), pref(len);
 
    int groups = bitLength / groupLength;
    int mask = len - 1;
    int negatives = 0, positives = 0;
 
    for (int c = 0, shift = 0; c < groups; c++, shift += groupLength) {
        // reset count array
        fill(count.begin(), count.end(), 0);
 
        // counting elements of the c-th group
        for (int i = 0; i < n; i++) {
            ++count[(a[i] >> shift) & mask];
 
            // additionally count all negative
            // values in first round
            if (c == 0 && a[i] < 0)
                ++negatives;
        }
        if (c == 0) positives = n - negatives;
 
        // calculating prefixes
        pref[0] = 0;
        for (int i = 1; i < len; i++)
            pref[i] = pref[i - 1] + count[i - 1];
 
        // from a[] to t[] elements ordered by c-th group
        for (int i = 0; i < n; i++) {
            // Get the right index to sort the number in
            int index = pref[(a[i] >> shift) & mask]++;
 
            if (c == groups - 1) {
                // We're in the last (most significant) group, if the
                // number is negative, order them inversely in front
                // of the array, pushing positive ones back.
                if (a[i] < 0)
                    index = n - index - 1;
                else
                    index += negatives;
            }
            t[index] = a[i];
        }
 
        // a[]=t[] and start again until the last group
        if (c != groups - 1) {
            for (int j = 0; j < n; j++)
                a[j] = t[j];
        }
 
    }
 
    // Convert back the ints to the double array
    for (int i = 0; i < n; i++)
        nums[i] = *(double*)(&t[i]); //重新把long long 的二进制转换为double
}

浮点数的基数排序肯定会比快速排序快，至于快多少我就没有测试了。

第二，IEEE754浮点数都是规格化浮点数。

规格化（normalized）浮点数是指尾数f的最高位非0。如果指数e的范围是无限的，则可以通过对尾数f移位并调整指数e的大小对v进行规格化；如果e的范围是有限的，则有些数并不能被规格化（f移位过多，导致调整后的e超出其范围）。有最小指数的不可规格化浮点数称为非规格化数（denormals）。[3]

当所有的数都是以规格化数或非规格化数表示时，他们是唯一的。[3]

IEEE754也能表示非规格化浮点数，但不在本文的讨论范围。

既然IEEE754浮点数都是规格化浮点数，则他们的f最高位都是1（非0），所以可以省略这一位。也就是说IEEE754双精度浮点数的尾数实际上有53位，只是最高位都是1，所以都省略掉了。

了解了这两点之后，我们就可以理解为什么将IEEE754双精度浮点数转换为十进制数的公式是下面这个样子了。

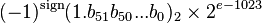
[1]

或者

[1]

在接下来的讨论中，假设一个浮点数为v，其尾数为$f_v$，指数为$e_v$，基为b（通常为2），则有$v=f_v\times b^{e_v}$。对于IEEE754 double，因为尾数省略了最高位1，所以有$hidden=2^{52}$，二进制串中的尾数为$f_{IEEE}$，真正的尾数为$f_v=hidden + f_{IEEE}$，真正的指数为$e_v=e_{IEEE}-bias$，所以有$v=f_v\times 2^{e_v}$。

舍入机制

因为浮点数并不能表示所有的实数，所以将实数映射到浮点数的时候，需要一个舍入机制，有两种舍入机制：

up：向上进位，使用$[x]^\uparrow$表示；

even：选择偶数，使用$[x]^\Box$表示，比如在十进制中，1.5→2、0.5→0；这是IEEE的默认策略。

当四舍五入的策略不重要时，使用$[x]^*$表示。我们使用$\widetilde x=[x]_p^s$来表示规格化浮点数$\widetilde x$（x上一根波浪线）的尾数位数（精度）为p，在规格化的过程中使用了s的四舍五入策略。

ULP

ULP的全称为unit in the last place，可以理解为尾数相差一个单位时，浮点数的差值。因为x被四舍五入到最接近x的值$\widetilde x$，所以有$|\widetilde x-x|\leqslant 0.5\times b^e=0.5ulp$。

邻居和边界

令$v=f_v\times b^{e_v}$是一个正浮点数，则v的前驱节点$v^-$是v的上一个可以表示的浮点数；v的后继节点$v^+$是v的下一个可以表示的浮点数。如果v是最小值，则$v^-=0$；如果v是最大值，则$v^+=v+(v-v^-)$。$v^-$和$v^+$都是v的邻居，他们和v具有相同的距离。

两个相邻的数$v_1$和$v_2$的边界为他们的算术平均$m=(v_1+v_2)/2$。根据定义，边界值是不能被表示的。每个浮点数v都有2个边界：$m^-=(v^-+v)/2$、$m^+=(v^++v)/2$。明显的，任何实数$m^-<w<m^+$都将四舍五入到v，也就是说在$(m^-,m^+)$之间的实数是无法用计算机表示的。

下面开始介绍Grisu算法，参考论文Printing Floating-Point Numbers Quickly and Accurately with Integers[3]。

自定义数据结构

本文使用整数来实现浮点数的转换，数据结构如下：

typedef struct diy_fp{
    uint64_t f;
    int e;
}diy_fp;

diy_fp中的f表示尾数，e表示指数。f的精度为q=64，高于IEEE754双精度浮点数的精度p=53。

diy_fp有两种运算，减法和乘法。减法为指数相等，尾数相减，结果可能没有规格化；乘法如下：

$x\otimes y=[(f_x\times f_y)/2^q ]^\uparrow \times 2^{e_x+e_y+q}$

乘法结果要四舍五入到64位，所以会有一些错误，但是错误不超过0.5ulp，结果可能没有规格化。

预计算10的幂

Grisu算法需要用到10的幂的规格化结果，提前计算好这些结果能加速Grisu运行。函数diy_fp cached_power(int k);能够直接返回$10^k$的规格化浮点数。

假设输入浮点数为v，其指数为e，需要寻找的10的幂即为$\widetilde{c_k}=f_{c_k }\times 2^{e_{c_k}}=[10^k ]_q^*$，且指数满足$\alpha \leqslant e_{c_k}+e \leqslant \gamma$。推导过程为：同时对$\widetilde{c_k}$两边取$log_{10}$得到$k=log_{10}(f_{c_k }\times 2^{e_{c_k}})$，将$e_{c_k}$的下界$e_{c_k}\geqslant\alpha-e$代入，得到$k=\lceil log_{10}(f_{c_k}\times 2^{\alpha -e})\rceil$，又因为$\widetilde{c_k}$所表示的10的幂的尾数精度为$q$，所以$f_{c_k}$的下界为$2^{q-1}$，代入前一个式子得到下式：

$k=\lceil log_{10}2^{\alpha -e+q-1}\rceil=\lceil (\alpha -e+q-1)\times 1/log_{2}10\rceil$

Grisu算法

假设浮点数v的指数是负数，则v可表示为$\frac{f_v}{2^{-e_v}}$ ，如果能找到一个t，使得$1\leqslant \frac{f_v\times 10^t}{2^{-e_v}}<10$，则v的十进制尾数为$\frac{f_v\times 10^t}{2^{-e_v}}$，十进制指数为-t；我们可以很容易获取$\frac{f_v\times 10^t}{2^{-e_v}}$的各位数字。

所以Grisu要解决的问题就是怎样快速的将$f_v\times 2^{e_v}$转换为$D\times 10^k$的形式，并且D尽量小。这样我们可以很容易的获取D的各位数字，和其十进制指数k。问题进一步转换为求k，使得$D=v\times 10^{-k}=f_v\times 2^{e_v}\times f_{c_{-k}}\times 2^{e_{c_{-k}}}$尽量的小，所以要让$e_{c_{-k}}$和$e_v$能尽量的抵消掉，这就是为什么在预计算10的幂中要求$\alpha \leqslant e_{c_k}+e \leqslant \gamma$，且$\alpha$和$\gamma$都比较小，但是论文表明$\alpha$和$\gamma$并不是越小越好。

Grisu算法描述

输入：精度为p的正浮点数v

前提：diy_fp的精度q≥p+2，且$\widetilde{c_k}=[10^k ]_q^*$已经提前计算好了。

输出：十进制字符串V，且满足$[V]_p^\Box=v$，也就是说再次读取字符串V时，能四舍五入成浮点数v。

过程：

1. 求v的规格化浮点数表示diy_fp w
2. 寻找满足$\alpha \leqslant e_c+e_w+q\leqslant \gamma$的10的幂$\widetilde{c_{-k}}=f_c\times 2^{e_c}=[10^{-k}]_q^*$
3. 计算乘积$\widetilde D=f_D\times 2^{e_D}=w\otimes\widetilde{c_{-k}}$
4. 定义$V=\widetilde D\times 10^k$，输出$\widetilde D$的十进制表示，字符’e’和k的十进制表示。

Grisu算法中，$\widetilde D$相当于v的十进制尾数，k相当于v的十进制指数。

Grisu2算法

Grisu算法虽然快，但是得到的结果并不是最短的，比如Grisu可能会把1.0打印成10000000000000000000e-19。Grisu2算法使用了额外的二进制位使得对于99%的输入都能输出最短的字符串表示。

主要长度

令v是一个正实数，n, l和s是整数，有$l\geqslant 1, 10^{l-1}\leqslant s\leqslant 10^l, v=s\times 10^{n-l}$，并且l越小越好，则s的前l个数字是v的主要数字（leading digits），l就是v的主要长度（leading length）。

通俗的说就是把V的不必要的前导和后尾0去掉后的长度，比如$1.23=123\times 10^{-2}$=$1230\times 10^{-3}$，但是$1230\times 10^{-3}$就多了一个不必要的后尾0，所以1.23的主要长度是3。

定理6.2

令x和y是2个实数，且$x\leqslant y$。令k是满足y mod $10^k\leqslant y-x$的最大整数，则有$V=\lfloor \frac{y}{10^k}\rfloor \times 10^k$满足$x\leqslant V\leqslant y$。并且V的主要长度（leading length）是所有在[x,y]范围内最小的。

Grisu2算法正是在Grisu的基础上，利用定理6.2输出了最短的长度。

Grisu2算法描述

输入：同Grisu算法

前提：diy_fp的精度q≥p+3，且$\widetilde {c_k}=[10^k ]_q^*$已经提前计算好了。

输出：十进制数字$d_i$，i属于[0,n]，和整数$\kappa $使得$V=d_0 ... d_n\times 10^\kappa $满足$[V]_p^\Box =v$

过程：

1. 计算v的边界$m^-$和$m^+$（$v\mp 0.5ulp$）
2. diy_fp $w^+=m^+$; diy_fp $w^-=m^-;$ 且$e_w^-=e_w^+$
3. 寻找满足$\alpha \leqslant e_c+e_w^++q\leqslant \gamma $的10的幂$\widetilde{c_{-k}}=f_c\times 2^{e_c}=[10^{-k}]_q^*$
4. 计算$\widetilde{M^-}=w^- \otimes \widetilde{c_{-k}}$；$\widetilde{M^+}=w^+ \otimes \widetilde{c_{-k}}$；$M_{\uparrow }^-=\widetilde{M^-}+1ulp$；$M_{\downarrow }^+=\widetilde{M^+}-1ulp$；$\delta =M_{\downarrow }^+-M_{\uparrow }^-$
5. 找到最大的$\kappa $使得$M_{\downarrow }^+ mod 10^{\kappa }\leqslant \delta $，并且定义$P=\lfloor \frac{M_{\downarrow }^+}{10^{\kappa }}\rfloor$
6. 定义$V=P\times 10^{k+\kappa }$，输出P的十进制数字和$K=k+\kappa $

Grisu2算法的前三步工作和Grisu算法类似，4,5步的工作近似求Grisu算法的$\widetilde D$的最短表示，利用的正是定理6.2，所以最终的指数是由k和$\kappa $两部分构成的。

该论文表示，Grisu2算法比sprintf快四倍左右，根据milo的测试[4] ，经过优化的Grisu2算法milo比sprintf快九倍，据说Google的V8 JavaScript引擎就是使用了Grisu算法，速度才很快的。

至于milo是怎么优化Grisu的，可以参考他的博客，完整的代码可以参考他的Github项目[4]。

关于完整全面的浮点数介绍，可以参考文献[5]。

参考：

[1]. https://en.wikipedia.org/wiki/Double-precision_floating-point_format

[2]. http://miloyip.com/images/grisu.jpg

[3]. Printing Floating-Point Numbers Quickly and Accurately with Integers第2节

[4]. dtoa-benchmark

[5]. What Every Computer Scientist Should Know About Floating-Point Arithmetic