上一篇博客主要介绍了逻辑回归的理论知识，这篇博客咱们用Python机器学习包sklearn中的LogisticRegression做一个分类的实例。

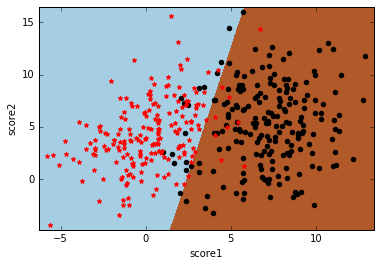
数据还是学生样本，只有两个特征，分别是两门课的分数score1和score2，类标号y表示这个学生是否能被录取。先上分类效果图：

完整的Python代码如下：

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145

# -*- coding: utf-8 -*-
"""
Created on Wed Nov 08 17:49:41 2017
 
@author: zhenlin
"""
 
import numpy as np  
import pandas as pd
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import classification_report
 
# 1. 构造数据
 
sample_number = 200
 
# 第一个高斯分布参数
mean1 = [0, 4] # 两个维度上的均值
cov1 = [[5, 3], [3, 10]] # 两个维度的协方差矩阵，必须满足对称半正定
 
# 第二个高斯分布参数
mean2 = [7, 5]
cov2 = [[7, 2], [2, 15]]
 
# 从两个二元高斯分布中随机采样数据点
class1_x1, class1_x2 = np.random.multivariate_normal(mean1, cov1, sample_number).T # .T表示转置
class2_x1, class2_x2 = np.random.multivariate_normal(mean2, cov2, sample_number).T
 
# 两个高斯分布对应两个类标号
data = [[class1_x1[i],class1_x2[i],0] for i in range(sample_number)]+[[class2_x1[i],class2_x2[i],1] for i in range(sample_number)]
 
# 填充到pandas中
data = pd.DataFrame(data,columns=['score1','score2','result'])
 
score_data = data[['score1','score2']]
result_data = data['result']
 
# 2. 训练模型
 
average_precision = 0 # 平均准确度
iters = 10 # 交叉验证次数
 
for i in xrange(iters):
    # 数据划分，80%用于训练，20%用于预测
    x_train, x_test, y_train, y_test = train_test_split(score_data, result_data, test_size = 0.2)
    # 构造默认逻辑回归模型
    model = LogisticRegression()
    # 训练
    model.fit(x_train, y_train)
    # 预测
    predict_y = model.predict(x_test)
    # 计算测试集上的准确度
    average_precision += np.mean(predict_y == y_test)
 
average_precision /= iters
  
# 3. 绘制分类面 - 法1
 
x1_min, x1_max = score_data['score1'].min() - .5, score_data['score1'].max() + .5
 
def generate_face(prob):
    y = -np.log(1.0 / prob - 1.0)
    n = 500
    x1 = np.linspace(x1_min, x1_max, n)
    # w1x1+w2x2+b=y
    x2 = (-model.coef_[0][0] / float(model.coef_[0][1])) * x1 + (y - model.intercept_) / float(model.coef_[0][1])
    return x1, x2
 
pos_data = data[data['result'] == 1]
neg_data = data[data['result'] == 0]
plt.scatter(x = pos_data['score1'], y = pos_data['score2'], color = 'black', marker = 'o')
plt.scatter(x = neg_data['score1'], y = neg_data['score2'], color = 'red', marker = '*')
 
face_04_x1, face_04_x2 = generate_face(0.4)
face_05_x1, face_05_x2 = generate_face(0.5)
face_06_x1, face_06_x2 = generate_face(0.6)
 
plt.plot(face_04_x1, face_04_x2)
plt.plot(face_05_x1, face_05_x2)
plt.plot(face_06_x1, face_06_x2)
plt.xlim(score_data['score1'].min(), score_data['score1'].max())
plt.ylim(score_data['score2'].min(), score_data['score2'].max())
plt.xlabel('score1')
plt.ylabel('score2')
plt.legend(['prob_threshold = 0.4', 'prob_threshold = 0.5', 'prob_threshold = 0.6'], loc='center left', bbox_to_anchor=(1, 0.865))
plt.show()
 
 
# 4. 绘制分类面 - 法2
 
pos_data = data[data['result'] == 1]
neg_data = data[data['result'] == 0]
 
h = 0.02
s1_min, s1_max = score_data['score1'].min() - .5, score_data['score1'].max() + .5
s2_min, s2_max = score_data['score2'].min() - .5, score_data['score2'].max() + .5
 
# 生成s1在[s1_min, s1_max]，且s2在[s2_min, s2_max]的网格数据点
# meshgrid含义参见：http://blog.sciencenet.cn/blog-791749-675394.html
s1, s2 = np.meshgrid(np.arange(s1_min, s1_max, h), np.arange(s2_min, s2_max, h))
# 把两个坐标的值按列拼在一起构成二维数据点
Z = model.predict(np.c_[s1.ravel(), s2.ravel()])
 
# 绘制边界和散点
Z = Z.reshape(s1.shape)
# 坐标点是(s1[i], s2[i])，对应颜色是Z[i]，颜色主题使用plt.cm.Paired
plt.pcolormesh(s1, s2, Z, cmap = plt.cm.Paired)
plt.scatter(x = pos_data['score1'], y = pos_data['score2'], color = 'black', marker = 'o')
plt.scatter(x = neg_data['score1'], y = neg_data['score2'], color = 'red', marker = '*')
plt.xlim(s1.min(), s1.max())
plt.ylim(s2.min(), s2.max())
plt.xlabel('score1')
plt.ylabel('score2')
plt.show()
 
# 5. 评估模型
 
# 对于测试数据，模型输出1的概率
answer = model.predict_proba(x_test)[:,1]
 
# 计算不同概率阈值下的P和R
precision, recall, thresholds = precision_recall_curve(y_test, answer)
 
# prob > 0.5的报告为1
report = answer > 0.5
 
print(classification_report(y_test, report, target_names = ['neg', 'pos']))
print('average precision: %f'%average_precision)
 
# 6. 绘制PRC曲线
 
# step阶跃图，在点(recall[i],precision[i])进行跳变
plt.step(recall, precision, color='b', alpha=0.2, where='post')
# 对PRC下方填充颜色
plt.fill_between(recall, precision, step='post', alpha=0.2, color='b')
 
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('2-class Precision-Recall curve')
plt.show()

下面将逐模块介绍代码细节，大神可以略过。

一、构造数据

数据的来源可以有很多种方式，sklearn包中自带7个Toy datasets，比如我们耳熟能详的鸢尾花卉数据集iris和手写数字数据集digits。为了学一学numpy，我们尝试自行构造数据集，这样也方便读者重复。我们可以从两个不同参数的高斯分布中采样相同数量的数据点，由于数据包含两个维度(score1, score2)，所以必须是二维高斯分布。二维高斯分布概率密度函数为：

参数包括：

\(\mu\)中的\(\mu_X\)和\(\mu_Y\)分别表示两个维度上的均值，\(\Sigma\)是这两个维度上的协方差矩阵，需要满足对称半正定。

numpy中的random.multivariate_normal可以从多元正态分布中进行采样，传入的参数包括均值mean, 协方差矩阵cov和采样数据点个数。比如本文中第二类数据点的均值为[7,5]，表示在score1维上的均值为7，在score2维上的均值为5，从图上黑点的横纵坐标分布也可以看出来；协方差矩阵为\(\begin{bmatrix}7 & 2\\2 & 15\end{bmatrix}\)，表示score1和score2上的方差分别为7和15，然后标准差的积再乘以相关系数等于2。用这些参数调用multivariate_normal就能得到对应二维平面\(x_1Ox_2\)上的数据点了。

最后，给两类数据点贴上不同的类标号，填充到Pandas中就大功告成了。Pandas中每一行表示一个样本，共有三列，分别表示score1、score2和result，其中result就是类标号。

二、训练模型

由于是直接调用sklearn中的逻辑回归函数，所以这一步非常简单。为了评估模型的准确度，我们做了一个交叉验证，即随机把数据分成80%用于训练，20%用于预测，重复10次，求预测准确度的平均值。这可以用模型选择中的train_test_split快速完成。

调用sklearn.linear_model.LogisticRegression()就能得到一个逻辑回归模型，该函数有很多参数，但是作为入门，所有参数都使用默认值。训练直接调用model.fit(x,y)，预测直接调用model.predict(x)。需要注意的是，model中带了很多成员变量，比如训练得到的分类面参数coef_和intercept_等，后面会用到。

三、绘制分类面（法1）

上一篇博客提到，虽然\(f(\mathbf{x})\)被Sigmoid函数映射到了概率空间，但逻辑回归的分类面还是\(f(\mathbf{x})=\mathbf{w^T x}+b=0\)。model通过fit函数训练之后，就能得到分类面的法向量\(\mathbf{w}\)（coef_）和截距\(b\)（intercept_），也就是说对于分类面\(w_1x_1+w_2x_2+b=0\)，我们已经知道了\(w_1\)、\(w_2\)和\(b\)，所以就可以在平面\(x_1Ox_2\)上画出这条直线了。具体的方法就是使用np.linspace先在\(x_1\)上选取足够多的点，代入\(w_1x_1+w_2x_2+b=0\)得到对应的\(x_2\)。该分类面如下图的prob_threshold=0.5。

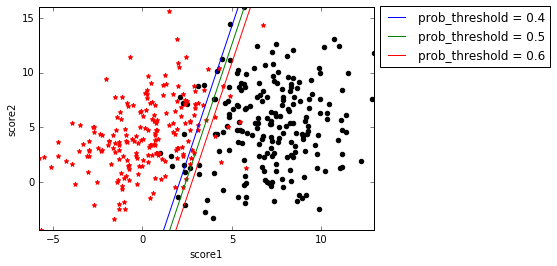
事实上，逻辑回归的分类面可以不止一个，我们上面得到的分类面是\(f(\mathbf{x})=0\)，代入到\(g(\mathbf{x})\)就是\(g(\mathbf{x})=0.5\)，也就是说当逻辑回归计算到的概率>=0.5分类为1，<0.5分类为0。但是我们也可以提高这个阈值，比如要求概率>=0.6分类为1，<0.6分类为0，这时，相当于我们对于分类为1的阈值提高了，要求更严格了，所以分类面应该向右边黑点方向移动。

求解prob_threshold=0.6的分类面也不难，令\(g(\mathbf{x})=0.6\)，得到\(f(\mathbf{x})=-lg(\frac{1}{0.6}-1)\)，剩下的过程和\(f(\mathbf{x})=0\)是一样的。由此得到的分类面如上图的prob_threshold=0.6那条线，确实在prob_threshold=0.5的右边。类似的，可以画出prob_threshold=0.4的分类面。

四、绘制分类面（法2）

还有一种简单粗暴的方法可以快速绘制出分类面。分类面的本质是在该分类面左右两侧的类标签不一样，如果我们把平面上所有点都预测一遍，对预测值为1的标上一种颜色，对预测值为0的标上另一种颜色，那么这两种颜色的交界处自然就是分类面了。

首先，我们使用np.meshgrid生成网格数据点，关于np.meshgrid的用法，这篇博客的介绍很好理解。然后对所有网格数据点调用model.predict进行预测。最后使用plt.pcolormesh的plt.cm.Paired颜色主题进行着色，即类标签为1的一种颜色，类标签为0的另一种颜色。最后把原始训练数据点画上去，就得到博客开篇的那张分类面图：

五、评估模型

model.predict是直接预测出类标号1或者0，而model.predict_proba是给出类标号分别为1和0的概率，用户可以自行根据prob_threshold进行分类。

1

precision, recall, thresholds = precision_recall_curve(y_test, answer)

precision_recall_curve的参数是正确答案y_test和model.predict_proba预测出来的概率，返回值分别表示不同threshold阈值下的precision和recall。sklearn官方的例子如下：

1
2
3

y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)

得到的结果如下：

1
2
3
4
5
6

precision
array([ 0.66..., 0.5 , 1. , 1. ])
recall
array([ 1. , 0.5, 0.5, 0. ])
thresholds
array([ 0.35, 0.4 , 0.8 ])

比如当threshold=0.4时，表示>=0.4分类为1，<0.4分类为0，则预测结果为[0,1,0,1]。正确率为预测为1的结果中对了几个1/2=0.5，召回率为召回了多少个正确答案为1的结果1/2=0.5。其他阈值的计算类似。

最后调用classification_report会算出不同类别的precision、recall和F1，以及对应的支持数据个数。

1
2
3
4
5
6
7
8

             precision    recall  f1-score   support
 
        neg       0.89      1.00      0.94        42
        pos       1.00      0.87      0.93        38
 
avg / total       0.94      0.94      0.94        80
 
average precision: 0.925000

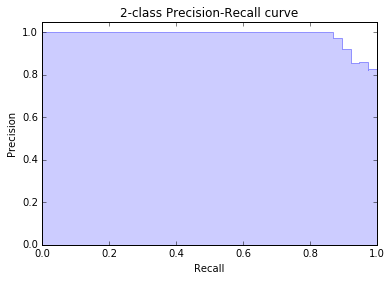
六、绘制PRC曲线

PRC曲线就是precision recall curve，由于上一步已经调用precision_recall_curve得到了不同阈值下的precision和recall，这一步直接拿来用就好了。为了防止画出来的曲线抖动形成毛刺，我们使用plt.step阶跃函数来绘制，起到平滑的作用。最后使用plt.fill_between填充曲线下方的面积。得到下图：

至此，整个示例讲解完毕。

如果要使用逻辑回归处理多分类问题，只需要构造好多标签的训练数据就好了，剩下的就交给模型自己处理。LogisticRegression的multi_class参数可以设置使用何种策略求解多分类问题，one-vs-rest (OvR)即构建k个二元分类器，multinomial即使用Softmax回归，默认使用OvR。

参考：