我们应该都听说过神经网络强大到能拟合任意一个函数,但细究起来很少有人能论证这个观点,这一章就用通俗易懂的图解方式来证明神经网络为什么能拟合任意一个函数。
开始介绍之前,有两点需要注意:
- 并不是说神经网络可以精确计算任意一个函数\(f(x)\),而是说当隐藏层神经元增加时,可以无限逼近\(f(x)\),比如对于任何一个输入\(x\),网络的输出\(g(x)\)和正确值\(f(x)\)的差小于某个阈值,\(|g(x) – f(x)| < \epsilon\);
- 神经网络拟合的是连续函数,而不是那种不连续、离散、急剧变化的函数。
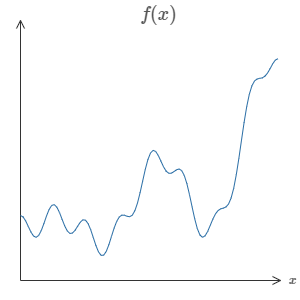
假设给定一个下图的连续函数,函数形式未知,本章将用图解的方式来证明,一个单隐层的神经网络就可以很好的拟合这个未知函数。
首先,假设我们的隐藏层只有两个神经元,激活函数使用Sigmoid,并且我们暂时只关注上面那个神经元的参数和输出。则通过调整该神经元的\(w\)和\(b\),可以得到不同形状的Sigmoid函数形式。
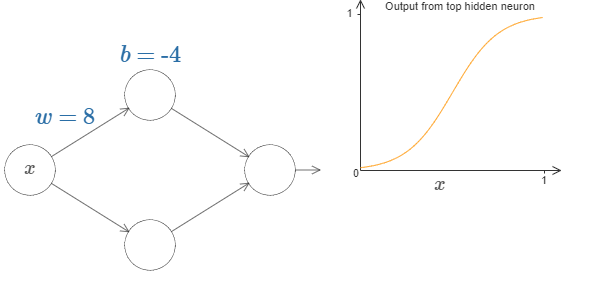
极端情况下,如果\(w\)很大而\(b\)很小,则可以用Sigmoid函数模拟阶梯函数:

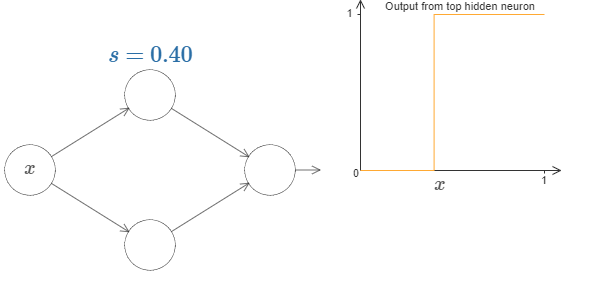
如果令\(s = -b/w\),则只用一个\(s\)就可以确定Sigmoid的函数图像:
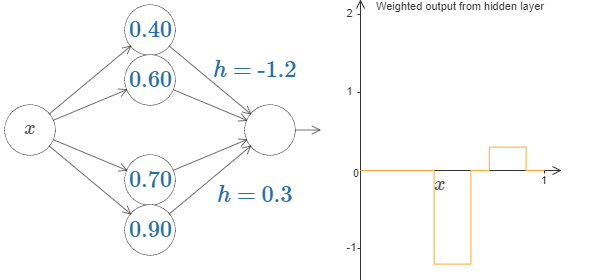
如果把隐藏层下面那个神经元也考虑进来,并且令隐藏层的两个神经元和输出层的神经元的连接权重互为相反数,则输出层未激活值\(z=w_1 a_1 + w_2 a_2\)的函数图像变成了一个神奇的鼓包,这个鼓包就是我们后续拟合任意函数的基本单元。根据严格的函数形式,还可以知道\(w_1\)和\(w_2\)的绝对值控制着鼓包的高度,\(s_1\)和\(s_2\)的值控制着鼓包的位置和宽度。大家可以去原始网页上体验一下作者给出的可交互版本,很有意思。

有了这个基本单元之后,我们可以通过增加隐藏层神经元的个数来增加鼓包的个数,比如再增加一对隐层神经元,可增加一个鼓包。虽然下图的例子中两个鼓包相互独立,但通过调整4个\(s\),可以让两个鼓包相连甚至交错,大家可以去原网页试一试。
继续增加隐层神经元个数,则可以继续增加鼓包的数量,如下图所示。
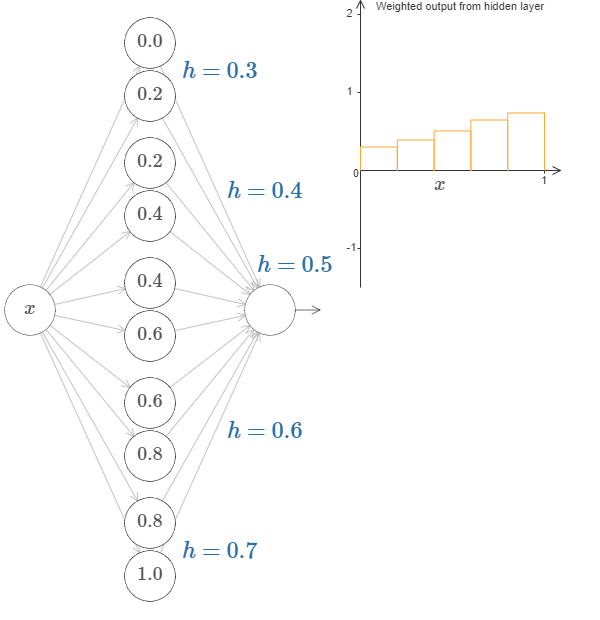
到这里想必大家马上知道了为什么神经网络能拟合任何一个函数了,如果隐层神经元足够多,则右图的小鼓包可以足够密,通过调整每个鼓包的高度,则无穷多个鼓包的顶点连线可以拟合任意一个函数。这和我们求函数积分(函数下方面积)时使用多个小矩形近似是一个道理!
所以对于本章开头的未知函数,我们通过调整不同鼓包的高度,可以使得小矩形面积之和与真实积分的差在\( \epsilon=0.4\)以内。如果无限增加隐层神经元个数,则可以无限逼近真实值。这就说明神经网络确实可以拟合任意一个函数。
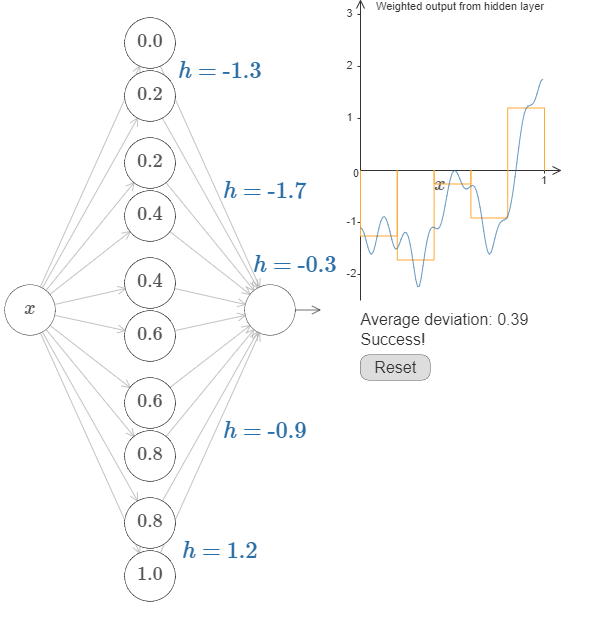
上述推导稍微需要注意的一点是,右图的输出是未激活函数值\(\sum_j w_j a_j\),而网络真正的输出是激活值\(\sigma(\sum_j w_j a_j + b)\)。这没有太大的关系,因为上面已经说明未激活输出能拟合任意函数,激活函数也是一个函数。增加激活函数就要求右图需要拟合激活函数和真实函数的嵌套函数。既然未激活输出能拟合任意函数,肯定能拟合这个嵌套函数\(\sigma^{-1} \circ f(x)\),再用激活函数作用一下\(\sigma\circ\sigma^{-1} \circ f(x)\),激活函数抵消了,正好得到\(f(x)\)。
如果输入是多维,或者输出是多维,都是类似的道理。这就说明神经网络确实可以拟合任意函数,真的很强大哦。