隐马尔可夫模型（Hidden Markov Model, HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。

先举一个简单的例子以直观地理解HMM的实质——韦小宝的骰子。

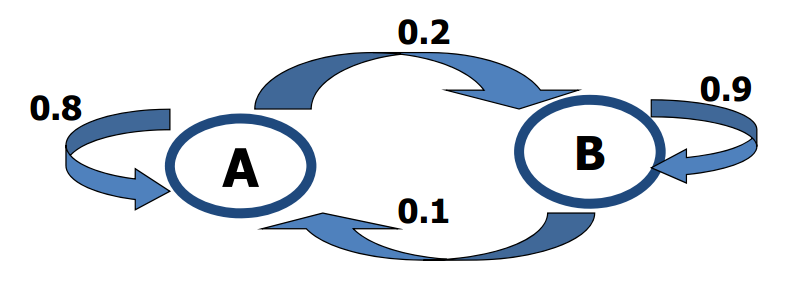
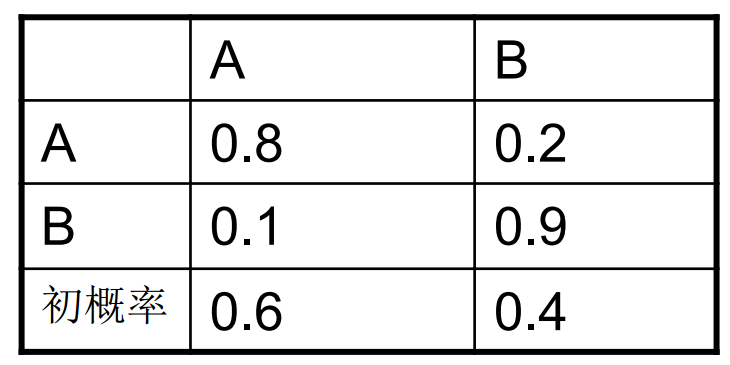
假设韦小宝有两个骰子，一个正常的骰子A，A以1/6的概率均等的出现每个点；一个不正常的骰子B，B出现5,6点数的概率为0.3，出现其他点数的概率为0.1。显然投掷B更容易出现大的点数。每次试验第一次投掷时，韦小宝会以0.4的概率出千（即投掷B）。但是在一次试验中，韦小宝不太可能一直出千，所以骰子会在A、B之间转换，比如这次投了B，下次可能会以0.1的概率投A。A、B之间的转移概率如下图。

某一次试验，我们观察到韦小宝掷出的骰子序列为$O=(1,3,4,5,5,6,6,3,2,6)$，请问韦小宝什么时候出千了。这个问题就可以通过HMM求解。

HMM有2个状态：

1. 观测状态。我们观察到的骰子序列称为观测状态$\mathbf{Y}=\{y_1,y_2,...,y_T\}$
2. 隐状态。隐含在每个观测状态里面的是隐状态$\mathbf{X}=\{x_1,x_2,...,x_T\}$

T是时间，也可以认为是观测的次数。HMM有3个参数：

1. 初始分布$\mathbf{\mu}=(\mu_i)$，$\mu_i=Pr(x_1=i)$，即第一次观测时，每个隐状态出现的概率
2. 转移概率矩阵$A=(a_{ij})$，$a_{ij}=Pr(x_{t+1}=j|x_t=i)$，即t时刻的隐状态为i，t+1时刻转移到隐状态j的概率
3. 发射概率矩阵$B=(b_{il})$，$b_{il}=Pr(y_t=l|x_t=i)$，即t时候隐状态为i的情况下，观测到状态为l的概率

参数$\mathbf{\lambda=\{\mu,A,B\}}$称为HMM的模型参数。具体到上面的例子，我们有初始分布和转移概率为：

发射概率为：

观测状态为$\mathbf{Y}=(1,3,4,5,5,6,6,3,2,6)$，问题就是求解出隐状态$\mathbf{X}$，此问题被称为HMM的解码问题，可以由著名的维特比算法（Viterbi algorithm）解决。

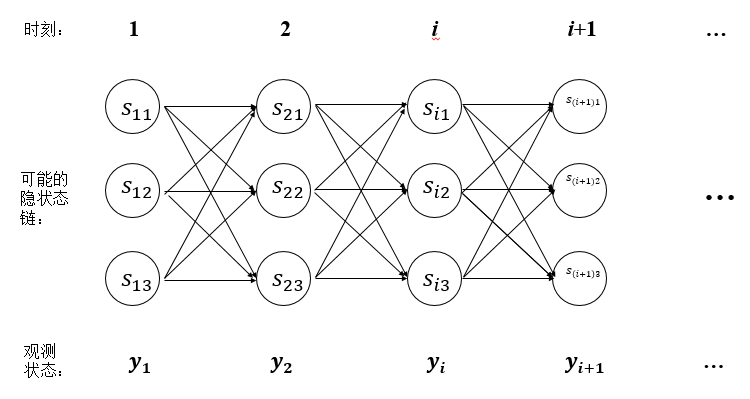
解码问题是要求出使得观测状态$Y$出现概率最大的隐状态$X$，假设有N个隐状态（本例为2），共有T个时刻（本例为10），则每个时刻有N个取值可能，则共有$N^T$条可能的隐状态链（本例为$2^{10}$）。我们需要求出每一条隐状态链下T个发射概率的乘积，然后取最大值，这是指数时间复杂度的（$O(N^T)$）。

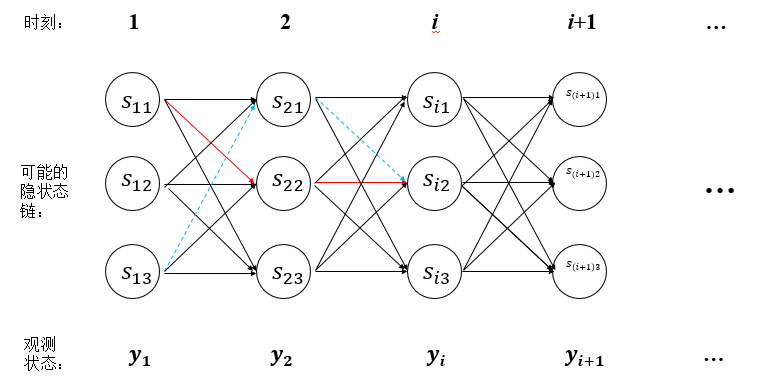
但是Viterbi算法是一个动态规划算法，只需多项式时间即可解决该问题。该算法的原理很好理解，假设我们求得到$s_{i2}$的最大概率路径为下图中的红线$s_{11}\rightarrow s_{22}\rightarrow ... s_{i2}$，则在求经过$s_{i2}$到$s_{(i+1)1}$的最大概率路径时，不需要再测试$s_{13}\rightarrow s_{21}\rightarrow s_{i2}\rightarrow s_{(i+1)1}$这条路径（下图蓝线），因为显然已经知道红线概率大于蓝线概率了。图中还有很多类似蓝线的路径都可以不用计算了，大大提高了求解速度。

因为计算第$i+1$时刻的累积概率只和第$i$时刻的概率有关，每次至多计算$N*N$个概率乘积（可以从$i$时刻的$N$个状态到达$i+1$时刻的某个状态，$i+1$时刻共有$N$个状态），最多计算T次（共T个时刻），所以时间复杂度降到了$O(N^2T)$。

下面我们形式化的描述Viterbi算法。

假设$\delta_t(i)$为$t$时刻取到隐状态$i$，且1~t的观测状态都符合观测值$Y$的各个路径的最大概率，即

$\begin{equation}\delta_t(i)=\underset{i_1,...,i_{t-1}}{\max}Pr(X_t=i,X_{t-1}=i_{t-1},...,X_1=i_1,Y_t=y_t,...,Y_1=y_1|\mathbf{\lambda})\end{equation}$

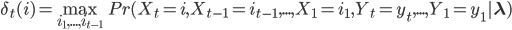
联系上图，可认为$\delta_t(i)$为红线。则递推公式为：

$\begin{equation}\delta_{t+1}(i)=b_{iy_{t+1}}\underset{j}{\max}(\delta_t(j)a_{ji})\end{equation}$

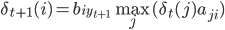
由$j$到$i$的转移概率，再乘上$i$发射$y_{t+1}$的概率。

在初始时刻$t=1$，有：

$\begin{equation}\delta_1(i)=\mu_ib_{iy_1}\end{equation}$

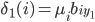
最后的全局最大概率为$\underset{j}{\max}\delta_T(j)$。为了得到完整路径，我们保留每一隐状态取得最大概率时的上一隐状态，即：

$\begin{equation}\psi_{t+1}(i)=j^*\end{equation}$

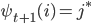
其中$j^*$要满足

$\begin{equation}\delta_{t+1}(i)=b_{iy_{t+1}}\delta_t(j^*)a_{j^*i}\end{equation}$

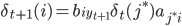
最后使用如下回溯法得到所有最佳隐状态：

$\begin{equation}X_T=i^*\in\{i:\delta_T(i)=\underset{j}{\max}\delta_T(j)\}\end{equation}$

$\begin{equation}X_t=\psi_{t+1}(X_{t+1})\end{equation}$

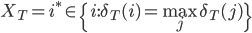
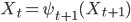
下面我们利用Viterbi算法来求解韦小宝的骰子这个例子。

$t=1$时，$y_1=1$，有$\delta_1(A)=0.6*1/6=0.1$，$\delta_1(B)=0.4*0.1=0.04$。

$t=2$时，$y_2=3$，有：

1. 隐状态为A：a）A->A有$\delta_2(A)=(1/6)*0.1*0.8=1.33*10^{-2}$；b）B->A有$\delta_2(A)=(1/6)*0.04*0.1=6.6*10^{-4}$。所以A->A，$\psi_2(A)=A$。
2. 隐状态为B：a）A->B有$\delta_2(B)=0.1*0.1*0.2=2*10^{-3}$；b）B->B有$\delta_2(B)=0.1*0.04*0.9=3.6*10^{-3}$。所以B->B，$\psi_2(B)=B$。

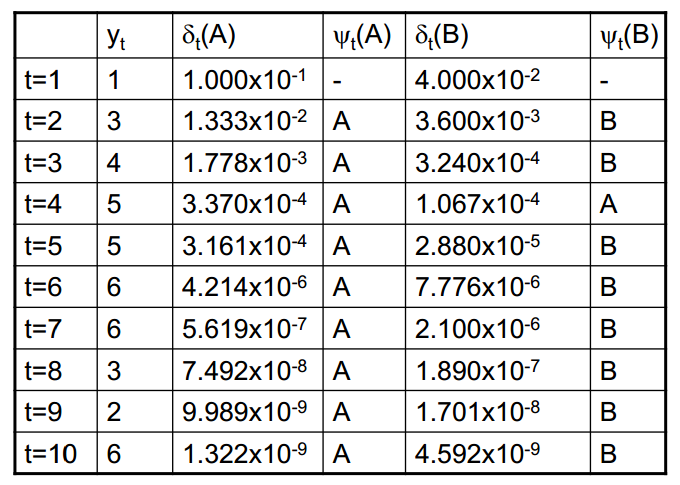
如此计算下去，可以得到如下表：

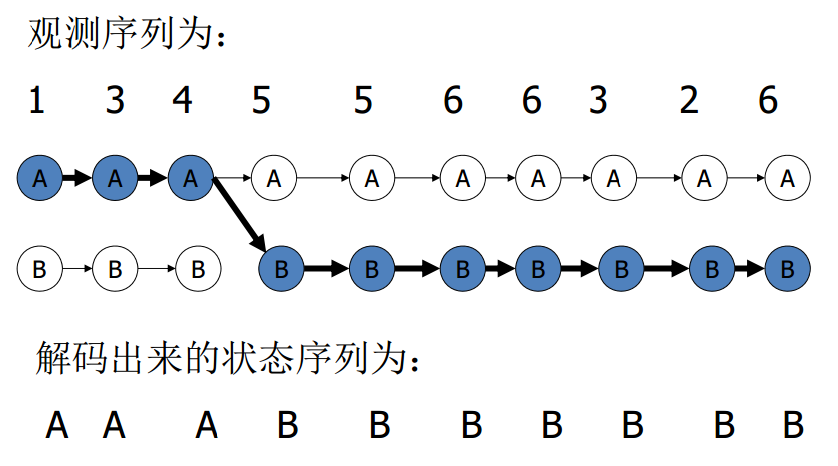
$t=10$时最大概率为$\delta_{10}(B)$，经过回溯得到最佳隐状态为：

所以HMM很神奇吧，可以抓住韦小宝从第5次开始就一直在出千，而且出千之后，掷出的点数大部分为5和6。

Viterbi算法还可用于解决语音识别或者拼音输入法。我们知道中文的一个拼音可以对应多个汉字，连续的一段拼音就能组成成千上万种可能的句子，哪一个句子才是最佳候选呢？我们可以把每个拼音当成观测状态，同音的汉字当成可能的隐状态。通过背景语料库统计得到每个汉字出现在词首的概率、汉字之间的转移概率和汉字与拼音之间的发射概率，这样我们就能得到模型参数，然后利用Viterbi算法求解出一个最佳的隐状态序列，这样就能完成一个简易的拼音输入法。

HMM在实际中主要有3个方面的应用，分别是：

1. 从一段观测序列$\mathbf{Y}$及已知模型$\mathbf{\lambda=(\mu,A,B)}$出发，估计出隐状态$\mathbf{X}$的最佳值，称为解码问题，这是状态估计问题。这篇博客讨论的就是这个问题。
2. 从一段观测序列$\mathbf{Y}$出发，估计模型参数组$\mathbf{\lambda=(\mu,A,B)}$，称为学习问题，就是参数估计问题。
3. 对于一个特定的观测链$\mathbf{Y}$，已知它可能是由已经学习好的若干模型之一所得的观测，要决定此观测究竟是得自其中哪一个模型，这称为识别问题，就是分类问题。

关于HMM的学习问题和识别问题，请听下回分解。