权重初始化

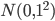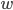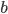在之前的章节中，我们都是用一个标准正态分布$N(0,1^2)$初始化所有的参数$w$和$b$，但是当神经元数量比较多时，会出现意想不到的问题。

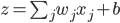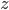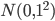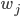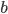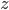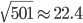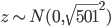假设一个神经网络的输入层有1000个神经元，且某个样本的1000维输入中，恰好有500维是0，另500维是1。我们目前考察隐藏层的第一个神经元，则该神经元为激活的输出为$z = \sum_j w_j x_j+b$，因为输入中的500维是0，所以$z$相当于有501个来自$N(0,1^2)$的随机变量相加。因为$w_j$和$b$的初始化都是独立同分布的，所以$z$也是一个正态分布，均值为0，但方差变成了$\sqrt{501} \approx 22.4$，即$z\sim N(0,\sqrt{501}^2)$。我们知道对于正态分布，如果方差越小，则分布的形状是高廋型的；如果方差越大，则分布的形状是矮胖型的。所以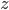$z$有很大的概率取值会远大于1或远小于-1。又因为激活函数是sigmoid，当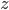$z$远大于1或远小于-1时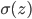，$\sigma (z)$趋近于1或者0，且导数趋于0，变化缓慢，导致梯度消失。

Continue reading →