首先介绍一下神经网络中不同数据集的功能,包括训练集、验证集和测试集。
训练集是用来训练网络参数的。当觉得在训练集上训练得差不多时,就可以在验证集上进行测试,如果验证集上的性能不好,则需要调整网络结构或者超参数,重新在训练集上训练。所以本质上验证集指导训练过程,也参与了训练和调参。为了防止网络对验证集过拟合,当网络在训练集和验证集上表现都不错时,就可以在测试集上进行测试了。测试集上的性能代表了模型的最终性能。
当然如果发现网络在测试集上性能不好,可能还会反过来去优化网络,重新训练和验证,这么说测试集最终也变相参与了调优。如果一直这么推下去的话,就没完没了了,所以一般还是认为用验证集对模型进行优化,用测试集对模型性能进行测试。
过拟合的含义就是网络在训练集上性能很好,但是在验证集(或者测试集)上的性能较差,这说明网络在训练集上训练过头了,对训练集产生了过拟合。为了便于叙述,本文没有验证集,直接使用测试集作为验证集对模型进行调优,所以主要考察网络在训练集和测试集上的性能表现。
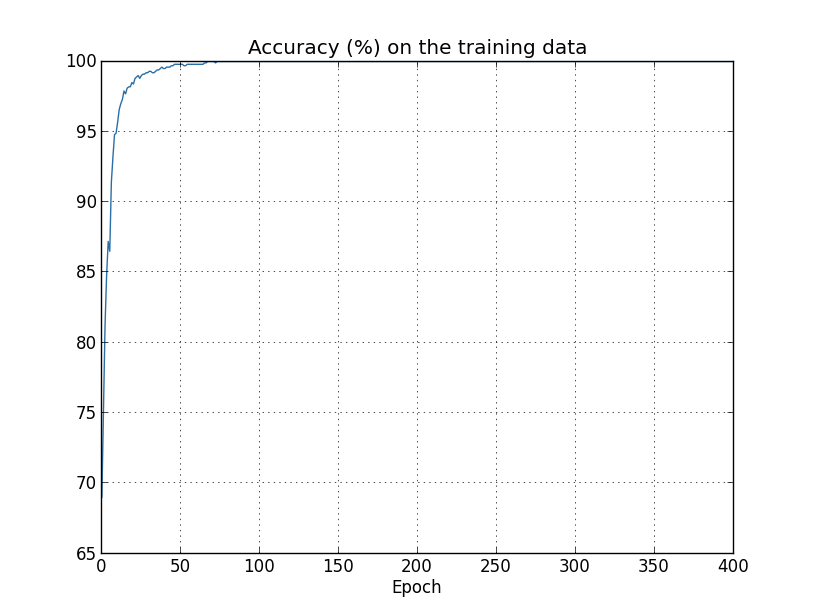
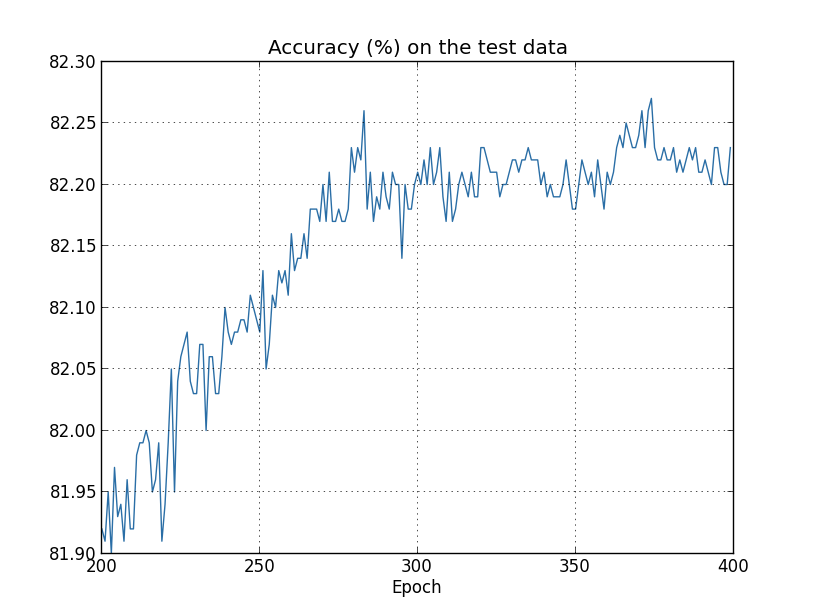
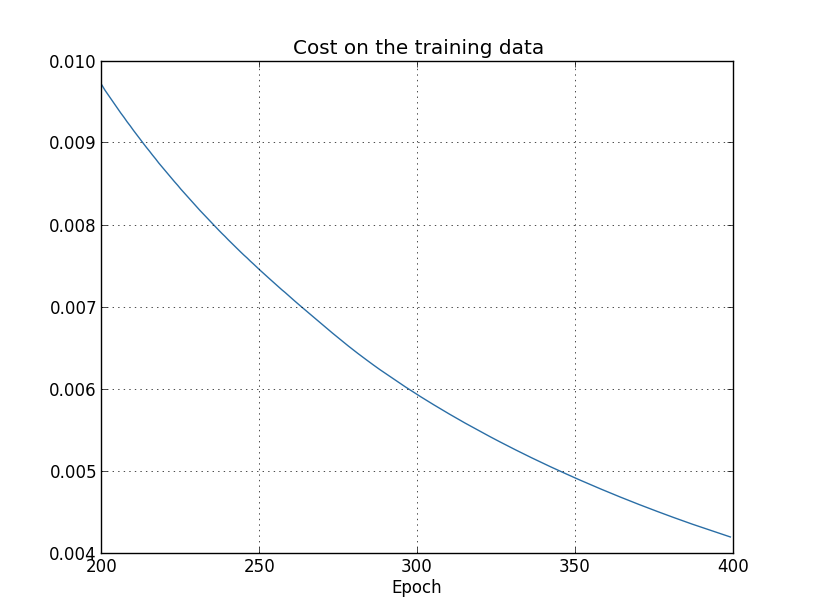
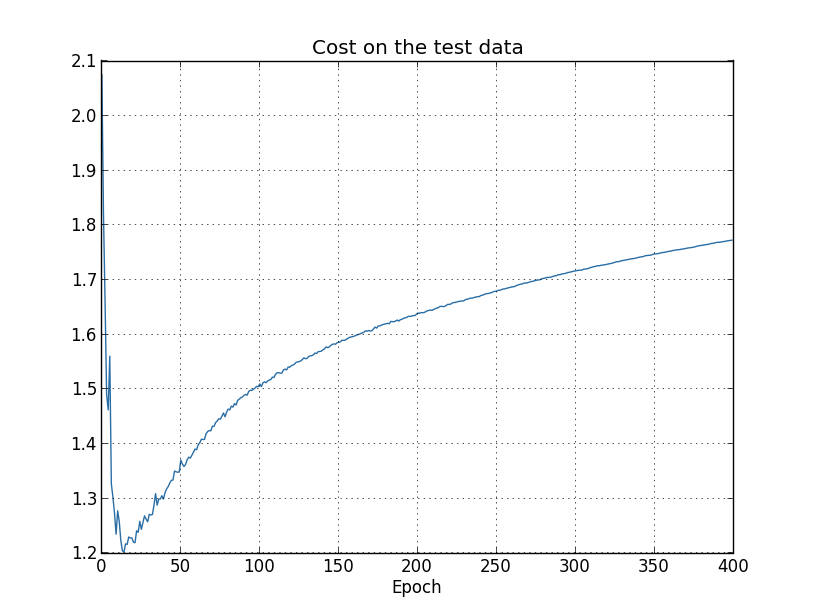
判断网络是否过拟合的方法就是观察网络在训练集和测试集上的accuracy和loss的变化曲线。对于accuracy,如果训练集的accuracy很高接近100%且收敛了,但测试集上的accuracy和训练集上的accuracy相差较大也收敛了(如下图收敛到82%左右),说明网络过拟合了。对于loss,如果训练集的loss一直在下降,但测试集的loss先下降后又上升,也说明网络过拟合了。这两种现象,虽然指标不同,但含义是一样的,即网络在训练集上的性能一直在提高甚至到完美水平,但在测试集上的性能提高到一定水平后不再变化甚至下降了。
不过下面几张图反应的过拟合epoch时间可能不一样,比如对于测试集上的accuracy,可能在280左右过拟合,但是对于测试集上的loss,在15和280左右都可以认为是过拟合了,尤其是15,loss最低,之后loss反升,可以认为是一个合理的过拟合的点。具体哪个epoch之后过拟合,取决于问题本身关注哪个指标,比如MNIST分类问题,可能关注分类accuracy,所以可重点关注测试集上的accuracy那个图,认为是280左右过拟合,因为200~280的accuracy还一直有提升,虽然提升很有限。
应对过拟合最好的方法就是增加训练数据,如果能把所有可能的数据都收集到,对所有数据产生过拟合,那相当于对所有数据都能预测得很好,那问题本质上已经解决了。
但是,在实际应用场景中,不可能收集到所有数据,而且数据往往是严重不足的,此时,应对过拟合主要有三种方法:正则化、Dropout和数据增强,下面分别介绍这三个部分。
正则化
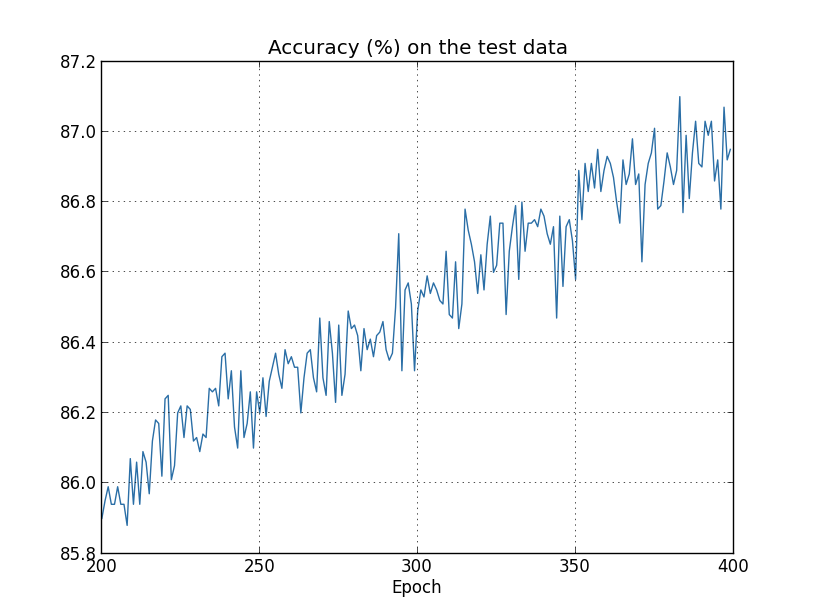
正则化的思路就是修改损失函数,使损失函数考虑模型复杂度。考虑正则化的损失函数的通用公式如下:
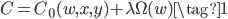
其中$C_0$为原始的没有正则化项的损失函数,比如MSE或者交叉熵损失等,$\Omega(w)$表示正则化项,即用来惩罚模型复杂度的,$\lambda$表示正则化参数,用来平衡$C_0$和$\Omega(w)$的重要性。
正则化又分为L2正则和L1正则,它们很类似,先详细介绍下L2正则。
举个例子,L2正则化后的损失函数如下:
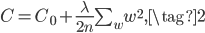
前半部分就是普通的损失函数(比如MSE或者交叉熵损失),后半部分就是L2正则。L2正则是对网络中的所有权重$w$求平方和($\vec w$的L2范数,所以叫L2正则),然后除以$2n$,其中$n$是训练样本数,除以2应该是为了后面求导方便。
(2)式的直观含义是,$\min C$的过程中,我不但希望损失函数本身$C_0$足够小,还希望网络的权重$w$也比较小,最好不要出现很大的$w$。如果$\lambda$越大,表示正则化越厉害,对大的$w$惩罚越严重。
加入L2正则后的梯度也很容易计算,如下:

对应的参数更新公式如下:
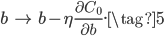

由(5)可知,偏移量$b$的梯度更新和没有正则化时是一样的,因为正则化并没有惩罚$b$,这个后面会解释为什么。由(7)可知,对$w$的梯度更新和没有正则化时很类似,只不过需要先对$w$进行缩放,缩放因子为$1-\frac{\eta\lambda}{n}$,因为训练样本$n$往往很大,所以缩放因子在(0,1),即先对$w$进行缩小,然后正常梯度下降,这种操作也被称为权值衰减。$\lambda$最好根据$n$的大小进行调整,如果$n$非常大的话,$\lambda$最好也大一些,否则权值衰减因子就会很小,正则化效果就不明显。
如果是mini-batch进行更新的话,公式也类似,梯度对mini-batch中的$m$个样本进行平均。
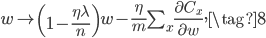
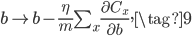
通过简单的L2正则,就能解决文章开头的过拟合问题,使得测试集上的accuracy在200~400个epoch时一直有提升。
正则化不仅能解决过拟合问题,还能使结果更加稳定。我们都知道,神经网络的参数是随机初始化的,很有可能不同的随机初始值收敛到的网络权重不一样,导致最终模型性能有差异。加入正则化后,对所有权重都有正则化约束,使得梯度下降在探索不同$w$的方向时,都能得到一定程度的更新,而不会说某个方向比较好就一直在那个方向探索。
那么正则化为什么能解决过拟合问题呢?从公式(1)可知,加入正则化之后,除了要优化网络对训练数据预测的准确度之外,还需要使得网络的权重$w$尽量小,权重越小则网络越简单,极端情况下如果权重等于0,则相当于少了一个参数,网络肯定更简单了。所以加入正则化之后,网络的复杂度降低了,网络的泛化能力就更强了,也就更不容易过拟合。
以一个很简单的(x,y)的二维数据拟合为例,我们既可以用一个九次函数$y = a_0 x^9 + a_1 x^8 + \ldots + a_9$完美拟合,也可以用一个一次函数$y = 2x$拟合。虽然九次函数能完美拟合,但是其最高次幂为9,一旦真实数据中有一些噪声,即x有一点噪声,则预测得到的y就会相差特别大,这其实就是非常严重的过拟合,即在训练数据上性能非常好,但在测试数据上性能可能较差,而且对噪声很不稳定。而一次函数虽然在训练集上不能完美拟合,但效果也不差,而且预想到它在应对有噪声的数据x时,也能预测得比较准确,所以一次函数的泛化效果更好,更不容易过拟合。



对应到神经网络中,$w$的大小可以类比成上面例子中的最高次幂,如果$w$很大,则x的微小扰动都可能造成网络输出的很大变化,就类似于上面的9次函数,很可能学到了数据中的局部噪声的特征。而$w$较小的网络,可能就没学到这些局部噪声的特征,而只是学到了数据中全局的(或者大部分数据都有的)、高频的特征,这其实是好事,这种网络在新的数据上的泛化能力就会更好,不易被噪声干扰。
其实哲学界还有一个“奥卡姆剃刀”原则,就是说如果一个数据集既能用简单模型解释,也能用复杂模型解释,那就尽量选择简单模型吧,简单就是美啊。
对于神经网络来说,还有一个很神奇的事情,就拿本文构造的神经网络为例,如果隐藏层有100个神经元,则大概有80000个参数,但是我们的训练数据集中只有50000张谱图,训练数据小于模型参数个数,按理说会导致严重的过拟合,但实际效果并没有,网络在测试集上的accuracy也很高。所以这很神奇,好像和机器学习中的经验风险最小化定理冲突。有人猜测这可能和多层神经网络有“自正则化”的效果有关。
最后,解释一下为什么正则化项中只有$w$没有$b$。因为每个神经元的操作是$\sigma(wx+b)$,$w$和$x$是乘法,影响更大,$b$对神经元输出的影响并不大,没必要正则化,当然强行对$b$正则也可以,只是和没对$b$正则效果差不多。说多了都是玄学,经验之谈。
L1正则和L2正则类似,只不过换成了对$w$的一范数,损失函数如下:
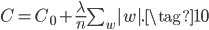
对$w$的权重更新公式如下,和(7)很类似,不细说了。
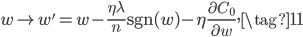
L1正则和L2正则都有一个权重衰减因子,虽然因子不同,但目的都是为了让$w$衰减,尽量小。他们的差别是L2衰减的是$w$的一个比例(公式(7),$w\left(1 - \frac{\eta \lambda}{n} \right)$),而L1衰减的是一个固定值(公式(11),$w-\frac{\eta \lambda}{n} \mbox{sgn}(w)$)。这就导致如果$w$本身很大的话,L1减的相对更少,而L2减的相对更多;如果$w$本身很小的的话,L1减的相对就更多,而L2减的相对更少。所以L1倾向于把小的$w$直接减到0,而对大的$w$不怎么减,而L2对所有$w$都一视同仁的减一定的比例。所以L1倾向于保留大的$w$,而直接把小的$w$正则为0,所以L1得到的非0权重可能更少,能得到稀疏模型,有利于特征选择。
对L1和L2正则的区别,比较常见的解释是二维情况下的图解,网上很多,比如:https://blog.csdn.net/jinping_shi/article/details/52433975。
Dropout
Dropout的做法和L1正则、L2正则很不一样,它不对损失函数进行修改,而是对网络结构进行修改。Dropout会在每个mini-batch训练时,随机删掉网络中一半的神经元(并不是真正的删除,而是暂时把对应的$w$设置为0)。它的效果相当于每次训练只用了一半的神经元,那么这次mini-batch和下次mini-batch相当于训练了不同的网络,最后预测时恢复所有的神经元。这样得到的预测结果相当于多个神经网络进行了average或者voting,使得预测结果更加鲁棒。比如有5个模型,其中3个模型预测对了,2个模型预测错了,做一下voting的话,就能得到正确的结果,而如果只是一个模型的话,如果刚好预测错了,那就错了。
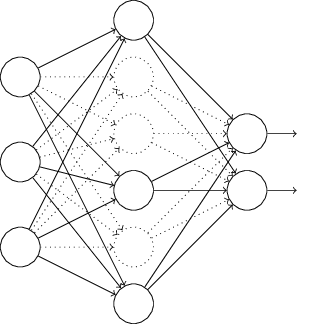
Dropout的另一个解释时,因为网络在训练时会随机删掉一半的节点,那么节点间的依赖关系就减弱了,迫使神经元依赖较少的信息也要得到比较好的预测结果,所以网络会更加鲁棒。Dropout在深层神经网络中,特别有用,能有效防止过拟合。不过也正因为此,dropout会增加训练收敛的时间,这是可以理解的。
数据增强
本博客开头就提到,解决过拟合最有效的方法就是增加训练数据集,但收集到的数据很少,有没有办法根据已收集的数据集,产生新的数据集呢,数据增强就是干这个的。
对图片数据来说,可做的数据增强包括:旋转、移位、翻转等。比如MNIST数据集,对一张手写数字图片4旋转15度,这张图片依然表示数字4,虽然人眼很容易识别旋转15度之后依然是4,但对网络来说,这个变化非常大,可以认为是一个新的样本。不过旋转角度不能太大了,比如6旋转变成9了,就不能标注成6了。
对于语音识别任务来说,数据增强可做的包括对语音添加背景噪声,快进,慢放等。总之,针对不同的任务,可以有不同的数据增强方法,基本原则就是增强之后的数据确实是现实世界中存在的数据,比如手写数字图片的轻微旋转,现实中就是有人写字写歪了一点;对语音进行快进,现实中就是有人说话快一点等。
最后总结一下,防止过拟合的方法包括:L2正则、L1正则、Dropout和数据增强。