权重初始化
在之前的章节中,我们都是用一个标准正态分布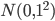 初始化所有的参数
初始化所有的参数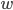 和
和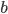 ,但是当神经元数量比较多时,会出现意想不到的问题。
,但是当神经元数量比较多时,会出现意想不到的问题。
假设一个神经网络的输入层有1000个神经元,且某个样本的1000维输入中,恰好有500维是0,另500维是1。我们目前考察隐藏层的第一个神经元,则该神经元为激活的输出为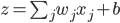 ,因为输入中的500维是0,所以
,因为输入中的500维是0,所以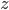 相当于有501个来自
相当于有501个来自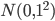 的随机变量相加。因为
的随机变量相加。因为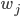 和
和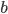 的初始化都是独立同分布的,所以
的初始化都是独立同分布的,所以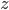 也是一个正态分布,均值为0,但方差变成了
也是一个正态分布,均值为0,但方差变成了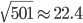 ,即
,即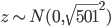 。我们知道对于正态分布,如果方差越小,则分布的形状是高廋型的;如果方差越大,则分布的形状是矮胖型的。所以
。我们知道对于正态分布,如果方差越小,则分布的形状是高廋型的;如果方差越大,则分布的形状是矮胖型的。所以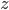 有很大的概率取值会远大于1或远小于-1。又因为激活函数是sigmoid,当
有很大的概率取值会远大于1或远小于-1。又因为激活函数是sigmoid,当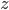 远大于1或远小于-1时,
远大于1或远小于-1时,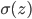 趋近于1或者0,且导数趋于0,变化缓慢,导致梯度消失。
趋近于1或者0,且导数趋于0,变化缓慢,导致梯度消失。


请注意,这里的梯度消失和之前介绍得梯度消失稍有不同,之前是说在误差反向传播过程中,损失函数对权重的导数中包含梯度消失项,所以可以通过更换损失函数来解决。但是这里的梯度消失并不是在误差反向传播过程中产生的,而是在正向传播产生的,跟损失函数没关系。
解决这个问题的方法很简单,根据上面的分析,如果输入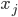 全为1,
全为1,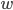 和
和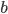 都来自
都来自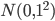 ,则
,则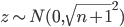 ,其中
,其中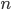 为输入样本的维度。要减小
为输入样本的维度。要减小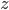 的方差,减小
的方差,减小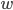 和
和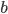 的方差就可以了。因为
的方差就可以了。因为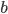 只有一个,对整体的影响不大,可以不修改
只有一个,对整体的影响不大,可以不修改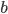 的分布,
的分布,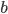 依然来自
依然来自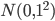 。把
。把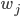 的分布修改为
的分布修改为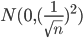 ,此时
,此时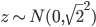 ,
,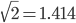 就非常接近1了,
就非常接近1了,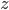 的分布也变成了一个高廋型的,梯度消失问题也就不存在了。
的分布也变成了一个高廋型的,梯度消失问题也就不存在了。
如果是开头的例子,输入维度为1000,其中500为0,500为1,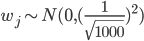 ,
,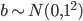 ,则
,则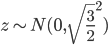 ,
,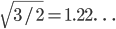 也是高廋型的,不会有梯度消失的问题。
也是高廋型的,不会有梯度消失的问题。
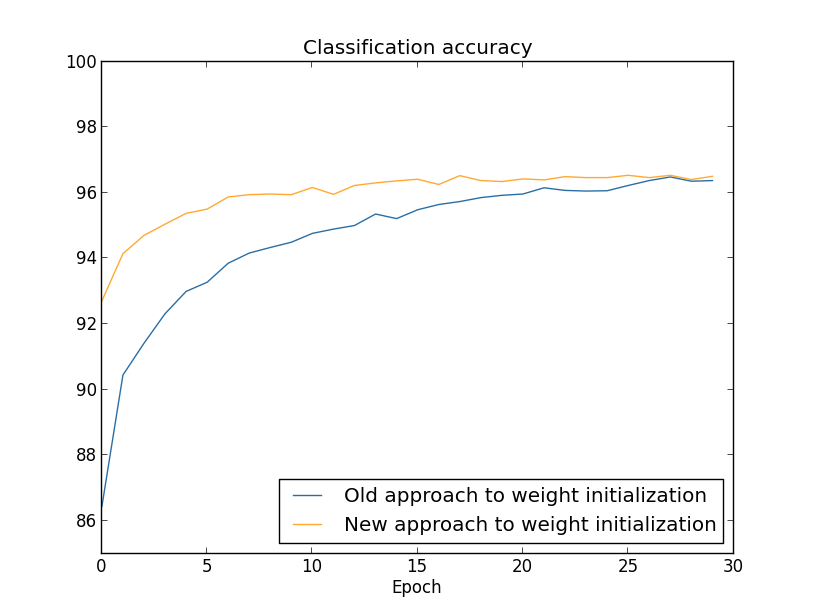
由下图可知,在新的权重初始化策略下,网络很快就收敛了,比之前的方法快很多。
怎样选择超参数
大原则:在网络优化的前期,尽量使网络结构、问题简单,以便快速得实验结果,不断尝试超参数取值,当找到正确的优化方向后,再慢慢把网络和问题变复杂,精细调整超参数。比如MNIST问题,开始可以减少训练数据,只取0和1的图片,做二分类;同时可以减少网络层数,验证集大小等,以便快速得到网络输出,判断网络性能变化。这样可以快速尝试新的超参数。
学习率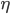
在误差反向传播中,学习率太大,虽然可以加速学习,但在后期可能导致网络震荡,无法收敛;学习率太小,导致学习速度太慢,训练时间过长。
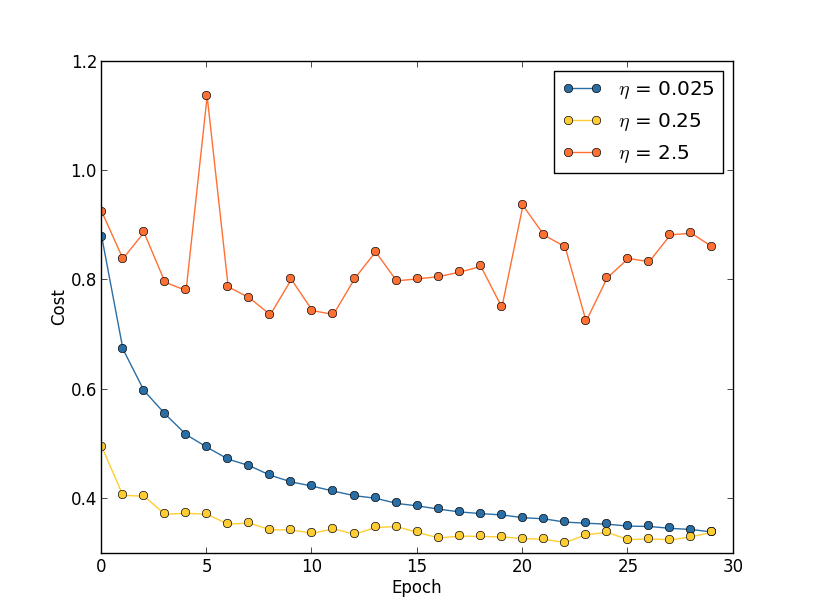
确定学习率的方法是:首先随便选定一个值,比如0.01,然后不断增大10倍:0.1, 1, 10, 100...如果发现cost曲线在震荡,说明选大了,要降低,直到找到一个比较合适的值。这个过程只要找到合适的数量级就可以了,不一定要非常精确。比如发现0.1是比较合适的,那么可以再尝试0.2,0.3...,如果发现0.5不错,可以设学习率为0.5的一半0.25,这样可以使得在后续epoch中,不容易发生震荡。最好的方法是可变学习率,即前期学习率稍大(0.5),后期学习率稍小(0.1)之类的。
epoch
no-improvement-in-ten rule,就是说如果模型在最近的10个epoch中,验证集的accuracy都没有提高,则可以stop了。在早期实验中可以这么做,后续精细优化时可以改变ten,比如no-improvement-in-20/30等。
正则化参数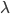
首先不要正则(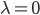 ),使用上面提到的方法确定学习率
),使用上面提到的方法确定学习率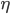 ,在确定的学习率情况下,正则
,在确定的学习率情况下,正则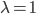 开始进行优化,比如每次乘以10或者除以10,观察验证集上的accuracy指标,找到正则化所在的合适的数量级,然后再fine-tune。
开始进行优化,比如每次乘以10或者除以10,观察验证集上的accuracy指标,找到正则化所在的合适的数量级,然后再fine-tune。
Mini-batch size
太小了,无法利用现有软件包的矩阵操作的优势,速度会很慢。极端情况下,如果mini-batch size=1,就是说每次只用一个sample做BP,则100次mini-batch=1会比一次mini-batch=100操作慢很多,因为很多软件包对矩阵操作有优化,而没有对for循环优化。太大了,则一次BP要很久,参数更新的次数也比较少。
其他技术
随机梯度下降SGD的变种
海森矩阵法
SGD优化的目标就是最小化损失函数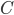 ,
,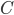 是所有参数
是所有参数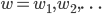 的函数,即
的函数,即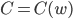 。希望能够通过改变
。希望能够通过改变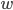 ,不断最小化
,不断最小化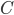 ,即找一个
,即找一个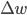 ,使得
,使得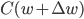 最小化。把
最小化。把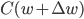 泰勒展开得到:
泰勒展开得到:

写成矩阵形式就是:
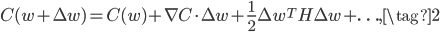
其中的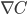 就是常规的梯度向量,
就是常规的梯度向量,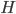 就是著名的海森矩阵,其中
就是著名的海森矩阵,其中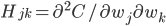 。如果把(2)中的高阶项扔掉,得到如下的近似等式:
。如果把(2)中的高阶项扔掉,得到如下的近似等式:
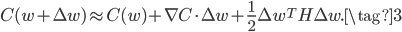
最小化(3)的右边,得:
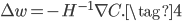
所以我们可以通过如下方式更新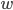 已达到最小化
已达到最小化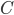 的目的,当然也可以给
的目的,当然也可以给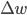 乘上学习率
乘上学习率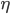 。
。

海森矩阵法有点像通过解析的方式最小化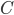 ,感觉上比SGD方法更精确靠谱。事实上,海森矩阵法确实比SGD方法收敛速度更快,但是因为在公式(4)中需要求解海森矩阵
,感觉上比SGD方法更精确靠谱。事实上,海森矩阵法确实比SGD方法收敛速度更快,但是因为在公式(4)中需要求解海森矩阵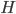 的逆矩阵
的逆矩阵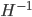 ,当网络的参数量很大时,求解过程会非常慢,导致海森矩阵法不实用。
,当网络的参数量很大时,求解过程会非常慢,导致海森矩阵法不实用。
基于动量的梯度下降
增加速度这个变量,个人不是太理解:
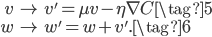
不同的激活函数
tanh是和sigmoid很像的一个激活函数,其函数形式为:
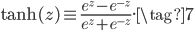
事实上,sigmoid函数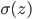 和
和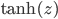 有线性关系:
有线性关系:
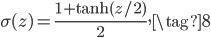
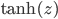 的函数图像如下,和sigmoid非常类似:
的函数图像如下,和sigmoid非常类似:

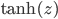 和sigmoid的主要区别就是值域不一样,前者值域为[-1,1],后者值域为[0,1]。这会导致什么差异呢?观察(BP4)这个公式,对于第
和sigmoid的主要区别就是值域不一样,前者值域为[-1,1],后者值域为[0,1]。这会导致什么差异呢?观察(BP4)这个公式,对于第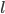 层的第
层的第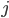 个神经元和第
个神经元和第 层的所有神经元的连接权重
层的所有神经元的连接权重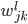 ,如果使用sigmoid激活,则
,如果使用sigmoid激活,则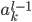 都是非负的,而这些梯度共用一个
都是非负的,而这些梯度共用一个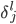 ,所以对于固定的
,所以对于固定的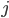 ,不同的
,不同的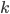 ,所有的梯度
,所有的梯度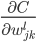 方向是一样的!这在无形中就减小了搜索空间。而如果用
方向是一样的!这在无形中就减小了搜索空间。而如果用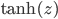 激活的话,不同的
激活的话,不同的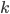 的
的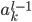 正负号可能就不一样,搜索空间更大,跟容易收敛。
正负号可能就不一样,搜索空间更大,跟容易收敛。


另一个比较常见的激活函数是ReLU激活函数,其函数形式如下:
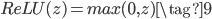
函数图像如下:

ReLU和Sigmoid、tanh很不一样,ReLU在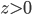 的方向上不会有梯度消失的问题。
的方向上不会有梯度消失的问题。
好了,第三章的内容就全部介绍完毕了,这一章介绍了很多调试神经网络的经验法则,没有太多的理论基础,相信随着这个领域的发展,神经网络的黑盒子会被慢慢打开。