本章我们将分析一下为什么深度神经网络难以训练的问题。
首先来看问题:如果神经网络的层次不断加深,则在BP误差反向传播的过程中,网络前几层的梯度更新会非常慢,导致前几层的权重无法学习到比较好的值,这就是梯度消失问题(The vanishing gradient problem)。
以我们在第三章学习的network2.py为例(交叉熵损失函数+Sigmoid激活函数),我们可以计算每个神经元中误差对偏移量$b$的偏导$\partial C/ \partial b$,根据第二章BP网络的知识,$\partial C/ \partial b$也是$\partial C/ \partial w$的一部分(BP3和BP4的关系),所以如果$\partial C/ \partial b$的绝对值大,则说明梯度大,在误差反向传播的时候,$b$和$w$更新就快。

假设network2的网络结构是[784,30,30,10],即有两个隐藏层,则我们可以画出在误差反向传播过程中,隐藏层每个神经元的$\partial C/ \partial b$的大小,用柱子长度表示。由下图可知,我们发现第二个隐藏层的梯度普遍大于第一个隐藏层的梯度,这会是一般现象吗,还是偶然现象?

既然梯度出现了层与层的差异,则可以定义第$l$层的梯度(如不加说明,则默认是误差$C$对偏移量$b$的梯度)向量的长度为$\| \delta^l \|$,比如$\| \delta^1 \|$表示第一个隐藏层中每个神经元的$\partial C/ \partial b$的绝对值之和,就是一范数,如果$\| \delta^l \|$越大,则说明这一层权重的更新越快。
由此,我们可以画出当有两个隐藏层时,$\| \delta^l \|$随epoch的变化情况:

当有三个隐藏层时:

当有四个隐藏层时:

我们发现,规律是惊人的一致,即越靠近输出层的隐藏层,$\| \delta^l \|$越大,即梯度更新越快;越靠近输入层的隐藏层,$\| \delta^l \|$越小,即梯度更新越慢。
这就会导致梯度消失的问题(The vanishing gradient problem):即在误差反向传播过程中,刚开始权重更新比较快,越到后面(越靠近输入层),则权重更新变得很慢,无法搜索到比较优的值。
所以,对于同样的network2,其他参数都不变,只是单纯增加网络层数,验证集上的准确率反而会下降!按理说网络层数增加,验证集上的准确率会上升,或者不变,至少不应该下降啊,因为最不济增加的网络层什么都不做,准确率应该一样才对,为什么反而下降了呢。虽然层数增加了,但因为上述梯度消失问题,靠近输入层的权重反而没学好,因为权重是随机初始化的,所以验证集上的准确率反而下降了。
那么,为什么层数增加会导致梯度消失问题呢,我们可以从BP的更新公式中一探究竟。
为了简化问题,假设我们的网络每一层只有一个神经元:

则根据BP的更新公式,可以计算得到
$\begin{eqnarray}\frac{\partial C}{\partial b_1} = \sigma'(z_1) \, w_2 \sigma'(z_2) \,w_3 \sigma'(z_3) \, w_4 \sigma'(z_4) \, \frac{\partial C}{\partial a_4}.\tag{1}\end{eqnarray}$
计算过程其实很简单,对照本博客开头的那张图,$\sigma'(z_4) \, \frac{\partial C}{\partial a_4}$就是(BP1),把(BP1)带入(BP2),就是不断乘以$w^{l+1} \sigma'(z^l)$,然后就能得到下图的公式。

我们在第三章时也曾介绍到梯度消失问题,当时提出的应对策略是采用交叉熵损失函数+Sigmoid,在求解梯度时可以把$\sigma'$抵消掉,以此来解决梯度消失的问题。但是请注意,当时求解的仅仅是误差对输出层的梯度,可以通过交叉熵损失函数+Sigmoid抵消$\sigma'$,对应到上图就是仅仅最后两项的$\sigma'(z_4) \, \frac{\partial C}{\partial a_4}$可以抵消$\sigma'$,即只有BP公式中的(BP1)可以抵消$\sigma'$。而如果误差继续反向传播,则其他层的梯度依然包含$\sigma'$项,由上图就可以看到,$\frac{\partial C}{\partial b_1}$除了最后的$\sigma'(z_4) \, \frac{\partial C}{\partial a_4}$抵消了一个$\sigma'$,前面还有3个$\sigma'$连乘。如果$\sigma$是Sigmoid激活函数的话,很容易就导致在Sigmoid两端,梯度更新缓慢的问题,然后又通过乘法放大了梯度消失的问题。
观察公式(1),我们发现梯度中包含很多$w_j \sigma'(z_j)$项相乘,如果$\sigma$是Sigmoid,则$\sigma'(z_j) \leq 1/4$,等号在$z_j=0$时取得;又因为权重随机初始化自$w_j\sim N(0,1)$,所以很容易有$|w_j| < 1$,这就导致$|w_j \sigma'(z_j)| < 1/4$,多个$w_j \sigma'(z_j)$项相乘,越乘越小,导致梯度消失。
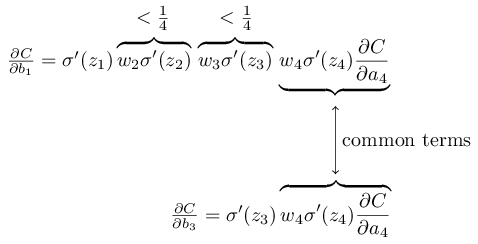
由下图可知,不同层的梯度,有部分是相同的,区别就在于$w_j \sigma'(z_j)$项乘的多少,所以这就能说明为什么反向传播得越多(越靠近输入层),梯度更新越慢。
上述$w_j \sigma'(z_j)$项连乘的问题不但会导致梯度消失问题,有时候还可能导致梯度爆炸(The exploding gradient problem)。比如假设令$w_1 = w_2 = w_3 = w_4 = 100$,令$b_i = -100 * a_{i-1}$,使得$z_i = w_i a_{i-1} + b_i = 0$,这就有$\sigma'(z_j) = 1/4$,进而有$w_j\sigma'(z_j)=100 * \frac{1}{4} = 25>1$。多个$w_j \sigma'(z_j)$项相乘就会越乘越大,导致梯度爆炸。
所以根源还是出现在多个$w_j \sigma'(z_j)$项相乘的问题上,导致BP梯度更新不稳定,有时候可能梯度消失,有时候可能梯度爆炸,这就导致深度神经网络训练起来有难度。也许把Sigmoid激活函数换成ReLU可以解决这个问题?