摘要
GCN模型是不是越复杂越好呢?这篇文章分析发现,GCN中常用的矩阵变换(feature transformation)和非线性激活函数(nonlinear activation)没有作用,甚至有反作用,据此作者提出了一个非常简单的GCN模型LightGCN,模型参数只有节点的embedding。这么简单的模型在推荐任务上,比大多数复杂模型的性能都要好,而且作者从理论分析了如此设计存在的若干好处。
简介
作者所在团队在2019年发表了一个NGCF的模型,该模型基于user和item的交互关系网络,使用GCN训练得到user和item的embedding,然后使用embedding相似度进行推荐。
简单来说,第k+1层的user和item的embedding使用如下公式计算。其中的W1是直接对embedding进行变换的矩阵,W2是对user和item点乘之后进行变换的矩阵;而σ是非线性激活函数。
以user为例,右边有两项,第一项是对user在第k层的embedding进行矩阵变换;第二项是邻居聚合。其中邻居聚合又有两项,第一项是对item的embedding进行矩阵变换;第二项是对user和item点乘之后进行矩阵变换。

作者发现,对于协同过滤任务来说,由于user和item都只有ID本身,没有很多的属性,所以并不需要复杂的矩阵变换和非线性激活函数。言下之意是,如果节点有丰富的属性信息的话,非线性变换和激活有用?感觉可以这么理解:有些属性重要,有些属性不重要,所以需要非线性激活函数进行识别?如果只有节点ID的话,ID的embedding的所有维度都是重要的,不需要非线性激活,直接线性加权聚合就行了。
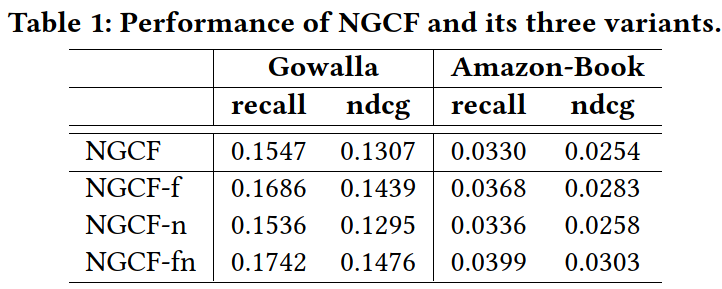
然后作者对NGCF模型进行了简单的消融实验,如下表所示,NGCF就是原始的NGCF,NGCF-f、-n、-fn分别表示去掉矩阵变换W1和W2、去掉非线性激活函数σ、同时去掉W1、W2和σ。很意外的是,-f、-n、-fn居然都比原始的NGCF效果好,而且-fn效果最好。说明对于只有user和item顶点,没有属性的网络来说,不用过于复杂的矩阵变换和非线性激活,效果反而更好。
按道理NGCF的参数空间比NGCF-f大,且前者能覆盖后者(只需要把W1和W2设置成单位矩阵),为什么前者的效果反而比后者差呢?作者进一步分析了两者训练时的loss和recall曲线,发现NGCF的参数空间虽然比NGCF-f大,但其收敛后的loss更大,recall更小。也就是说训练效果反而不如NGCF-f。作者认为,加入过多的矩阵变换和非线性变换,导致模型过于复杂,难以训练到较好的效果。据此,作者提出了一个更简单的模型LightGCN,具体看下一节介绍。
方法
既然前面分析说矩阵变换和非线性激活函数会起副作用,LightGCN的方法非常简单,就是把这两个操作去掉。如公式3所示,每个节点的embedding表示直接等于其邻居的embedding的线性加权求和,既没有矩阵变换,也没有非线性激活函数,如此的简单。而且,对比公式3和公式1可知,LightGCN没有显式使用自回路,即计算某个节点的embedding的时候,只用了其邻居的embedding,没有用自己的embedding;而NGCF在公式1中使用了自回路。

其网络结构图如下:

最后,节点的最终embedding等于其各层embedding的加权求和。如公式4所示,权重系数α可以手工指定,也可以使用注意力网络来自动学习。为简便起见,本文直接设置为等权重,所有系数都等于1/(K+1),相当于所有层embedding求平均。

节点最终embedding等于各层embedding的加权求和有如下三个好处:
- GNN存在over-smoothing的问题,即随着网络层数越深,深层网络的输出结果趋向于相同。即所有节点的最后一层的输出有可能很接近。而如果把所有层加起来的话,能一定程度上缓解这个问题
- GNN不同层捕获的语义信息不一样,使用所有层输出能增强表达能力,这个和CNN的道理是类似的。
- 所有层embedding求和可以捕获自回路的信息。也就是说虽然公式3没有显式使用自回路,但计算顶点最终embedding时(公式4)可以隐含自回路的信息,这个后面会给出证明。
除此之外,由于LightGCN很简单,所以也很好训练,更容易收敛,收敛效果更好。总之,虽然LightGCN很简单,但它很强大,而且有很多好处。
模型分析
接下来,作者分析了为什么LightGCN可以学习到自回路,其证明思路是这样的。另一篇工作SGCN和这篇工作很像,也做了很多简化,且显式添加了自回路。作者通过分析发现LightGCN可以表达SGCN的形式,间接说明LightGCN隐含可以考虑自回路。下面是具体的证明过程。
首先定义user和item的交互矩阵 $\mathbf{R}\in \mathbb{R}^{M\times N}$,其中M和N分别表示user和item的个数。 $\mathbf{R}_{ui}$ 为1表示u和i有交互,等于0表示没有交互。则全图的邻接矩阵可以表示为公式6:

公式3的矩阵形式可以表示成公式7,其中矩阵D为度矩阵。对照下原始的GCN公式,其实就是把原始GCN的变换矩阵W和非线性激活函数σ去掉了。

由于LightGCN是将多层embedding加权求和,所以最终结果是公式8:

然后作者对SGCN的公式进行了简单的变换,发现形式上和公式8是一致的,所以LightGCN也能隐含学习到自回路特征。
此外,作者还分析了另一个模型APPNP,APPNP借鉴pagerank的思想,可以缓解GNN过深带来的over-smoothing问题。然后作者如法炮制,对APPNP的公式进行变换,发现也和公式8等价,所以LightGCN也能缓解GNN的over-smoothing问题。其实这个从LightGCN不只使用最后一层,而是使用所有层embedding就能得到这个结论,不需要这么大费周章证明。
实验
最后是实验环节。作者将LightGCN和本文开头提到的NGCF进行了对比,实验结果表明,LightGCN的性能相比NGCF有显著提升,而且比NGCF-fn也高。作者提到,虽然NGCF-fn已经去掉了矩阵变换和非线性激活函数,但NGCF-fn仍然还有自回路、user和item的点积、dropout等等,还是比较复杂,不好训练。而LightGCN非常简单,只有embedding和邻居的线性加权,所以LightGCN还是比NGCF-fn好。真的很神奇啊,照这个说法,难道连dropout也会起副作用?
此外,在消融实验中,作者还对比了LightGCN和LightGCN-single,LightGCN-single是只用LightGCN的最后一层作为节点的embedding。作者发现,当网络层数增大到4层时,LightGCN-single性能显著下降,出现了over-smoothing的问题。而LightGCN由于多层组合的操作,不会有over-smoothing的问题。考虑到性能和收益,LightGCN使用了3层神经网络。
评价
结果有些意外,LightGCN这么简单的模型,效果居然比复杂模型还要好?感觉即使是NGCF,模型也不复杂啊,和CV、NLP那些大模型相比简单多了,怎么就训练不好了呢?难道是GNN特有的现象?
感觉和数据有关,本文测试的数据是只包含user和item顶点,顶点没有属性。如果是属性图的话,也许结论会有变化。
不过至少提供了调参的思路:去掉矩阵变换、去掉非线性激活函数、甚至是去掉dropout。。。另外重要的一点是,不要只用最后一层的embedding,而是组合所有层的embedding进行加权求和。
另外,本文开篇提到的NGCF和本文是同一批作者,自己批判自己一年前发表的工作,不免让人担心这篇工作的可靠性。。。以及当时的NGCF难道没有做本文开篇的消融实验吗?难道不应该吗?