上一回介绍了HMM的解码问题,今天我们介绍HMM的学习问题和识别问题,先来看学习问题。
正如上一回结束时所说,HMM的学习问题是:仅已知观测序列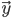 ,要估计出模型参数组
,要估计出模型参数组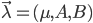 ,其中
,其中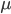 为初始概率分布向量,
为初始概率分布向量,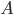 为转移概率矩阵,
为转移概率矩阵,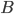 为发射概率矩阵。
为发射概率矩阵。
算法设计
求解HMM的参数学习问题,就是求解如下的最优化问题:
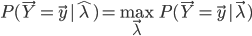
也就是找一个参数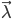 ,使得模型在该参数下最有可能产生当前的观测
,使得模型在该参数下最有可能产生当前的观测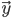 。如果使用极大似然法求解,对于似然函数
。如果使用极大似然法求解,对于似然函数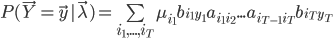 而言,这个最大值问题的计算量过大,在实际中是不可能被采用的。为此,人们构造了一个递推算法,使其能相当合理地给出模型参数
而言,这个最大值问题的计算量过大,在实际中是不可能被采用的。为此,人们构造了一个递推算法,使其能相当合理地给出模型参数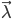 的粗略估计。其核心思想是:并不要求备选
的粗略估计。其核心思想是:并不要求备选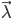 使得
使得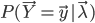 达到最大或局部极大,而只要求使
达到最大或局部极大,而只要求使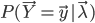 相当大,从而使计算变为实际可能。
相当大,从而使计算变为实际可能。
EM算法
为此,我们定义一个描述模型“趋势”的量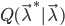 代替似然函数
代替似然函数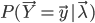 ,其定义为:
,其定义为:
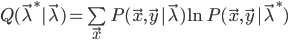
利用在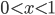 时,不等式
时,不等式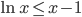 成立,可以证明:
成立,可以证明:
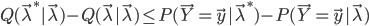
由此可见,对于固定的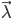 ,只要
,只要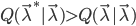 ,就有
,就有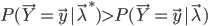 。于是想把模型
。于是想把模型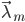 修改为更好的模型
修改为更好的模型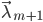 ,只需找
,只需找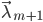 使得:
使得:
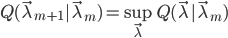
即只要把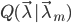 关于
关于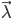 的最大值处取成
的最大值处取成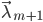 ,就有
,就有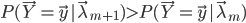 。
。
这样得到的模型序列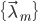 能保证
能保证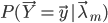 关于
关于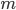 是严格递增的,虽然在这里还不能在理论上证明
是严格递增的,虽然在这里还不能在理论上证明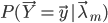 收敛到
收敛到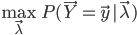 ,但是当
,但是当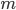 充分大时,
充分大时,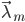 也还能提供在实际中较为满意的粗略近似。
也还能提供在实际中较为满意的粗略近似。
综上论述,我们把如上得到的近似模型列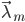 的方法归结为两个步骤:
的方法归结为两个步骤:
- E步骤(求期望):计算
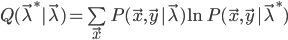
- M步骤(求最大):求
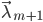 使
使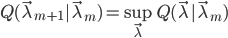
这两个步骤合起来构成的算法,称为期望最大化(Expectation-maximization, EM)算法。EM算法是针对在测量数据不完全时,求参数的一种近似于最大似然估计的统计方法。
Baum-Welch算法
隐Markov模型中的M-步骤的解可以有显式表示,这就是一组把模型参数修改为新的模型参数的递推公式,这组公式正好是在隐Markov模型中普遍应用的著名的Baum-Welch公式。
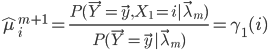


Baum-Welch算法用到了如下几个公式:
- 向前算法,
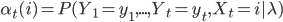 ,满足前
,满足前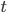 个状态,推进到满足前
个状态,推进到满足前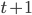 个状态(
个状态(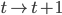 ):
):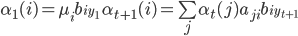
- 向后算法,
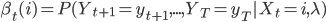 ,满足后
,满足后 个状态,推进到满足后
个状态,推进到满足后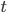 个状态(
个状态(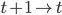 ):
):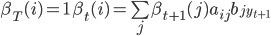
- 向前向后算法,满足所有观测状态,且
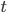 时刻的隐状态为
时刻的隐状态为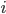 :
:
- 以及记号
算法流程
最后,我们可以将Baum-Welch公式应用于EM算法中的M步骤,来逐步改进模型参数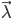 。为了使训练结果更加可信,通常应该有多条观测序列。假设输入为所有
。为了使训练结果更加可信,通常应该有多条观测序列。假设输入为所有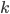 次观测序列集合
次观测序列集合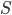 和收敛阈值
和收敛阈值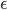 ,输出为训练得到的模型参数
,输出为训练得到的模型参数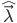 ,则基于Baum-Welch公式的EM算法求解HMM学习问题的伪代码如下:
,则基于Baum-Welch公式的EM算法求解HMM学习问题的伪代码如下:
 现在要求解另一个韦小宝的骰子的问题:韦小宝有两个有偏的骰子A,B,A,B掷出相同点数的概率不同,每次韦小宝随机拿一个骰子并投掷,记录下正面朝上的点数,重复100次,得到一条长度为100的点数序列,如此重复100次,得到100条类似的序列。现只给定这100条点数序列,要求解出韦小宝每次投掷的是哪个骰子,并分析这两个骰子有什么区别。
现在要求解另一个韦小宝的骰子的问题:韦小宝有两个有偏的骰子A,B,A,B掷出相同点数的概率不同,每次韦小宝随机拿一个骰子并投掷,记录下正面朝上的点数,重复100次,得到一条长度为100的点数序列,如此重复100次,得到100条类似的序列。现只给定这100条点数序列,要求解出韦小宝每次投掷的是哪个骰子,并分析这两个骰子有什么区别。
这就是一个典型的HMM的参数学习问题,利用上述伪代码可以很快的求解出模型参数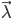 ,A,B的发射概率就是它们的不同点。
,A,B的发射概率就是它们的不同点。
HMM的识别问题是:对于一个特定的观测链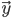 ,已知它可能是由已经学习好的若干模型之一所得的观测,要决定此观测究竟是得自其中哪一个模型,这称为识别问题。
,已知它可能是由已经学习好的若干模型之一所得的观测,要决定此观测究竟是得自其中哪一个模型,这称为识别问题。
判决步骤:
- 根据参数求出在每一个模型中,出现给定样本的概率
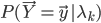 ,归一化就得到给定样本来自每个模型的概率
,归一化就得到给定样本来自每个模型的概率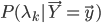 。
。 - 利用贝叶斯原理,就可以得到最好模型的猜测。
本博客开头提到,要求解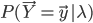 需要指数时间(
需要指数时间(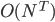 ):
):
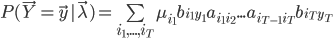
所以可以利用向前算法(式(10))或者向后算法(式(11)),对应的结果分别为:
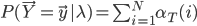
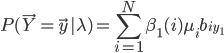
然后利用贝叶斯公式得到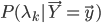 ,使结果最大的
,使结果最大的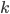 即为所求模型。
即为所求模型。