马尔可夫聚类算法(The Markov Cluster Algorithm, MCL)是一种快速可扩展的基于图的聚类算法。它的基本思想为:在一个稀疏图G中,如果某个区域A是稠密的(是一个聚类),则在A中随机游走k步,还在A内的概率很大,也就是说,A内的k步路径(k-length path)很多。所以我们可以在图中随机游走k步,如果某个区域连通的概率很大,则该区域是一个聚类。随机游走的下一步只和当前所处节点有关,也就是说这是一个马尔可夫的随机游走过程。
我们用一个例子来演示马尔可夫聚类算法的过程。
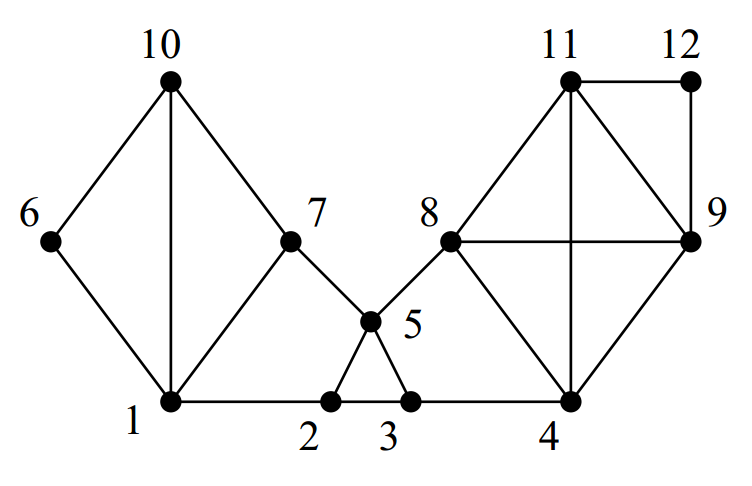
上图是一个很小的网络,我们用肉眼大概能看出有三个聚类,分别是左边的{1,6,7,10},中间的{2,3,5}和右边的{4,8,9,11,12}。我们用MCL看看结果如何。
为了随机游走,我们常用邻接矩阵来表示图,如果i,j有边,则N[i][j]=1,否则N[i][j]=0。又随机游走可能有自回路,所以加上单位矩阵I,得到矩阵N+I。
MCL有两个关键的步骤,分别是Expansion和Inflation。
Expansion就是不断对矩阵进行幂次运算,相当于随机游走。假设随机游走了2步,则得到如下图的关联矩阵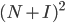 ,第1行第10列为4,说明1到10的2-length path有4条:1→6→10,1→7→10,1→1→10,1→10→10。随机游走k步之后,
,第1行第10列为4,说明1到10的2-length path有4条:1→6→10,1→7→10,1→1→10,1→10→10。随机游走k步之后,![(N+I)^k[i][j]](https://bitjoy.net/wp-content/plugins/latex/cache/tex_39b4ac10ae8ec43f4b08ada9ffa7f3c4.gif) 越大,说明
越大,说明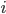 和
和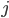 之间的连通性越强。
之间的连通性越强。
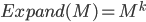
Inflation是为了增强更强的连接,减弱更弱的连接,只有这样才能得到边界比较明确的聚类。MCL的做法是对元素做幂次运算,然后按列归一化,公式为:
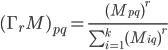
参数经验值是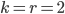 。不断做Expansion和Inflation操作,直到算法收敛,得到若干个聚类。中间过程请点此查看,下图为最终结果。
。不断做Expansion和Inflation操作,直到算法收敛,得到若干个聚类。中间过程请点此查看,下图为最终结果。
从图中可以看出,和1有边的只剩下6,7,10了,所以得到聚类{1,6,7,10},同理能得到聚类{2,3,5}和{4,8,9,11,12} ,和我们肉眼得到的结果是一致的。
MCL算法的原理很简单,得到的聚类效果也不错。下面总结一下MCL的算法过程:
- 给定无向图G,Expansion和Inflation的参数
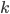 和
和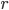
- 生成G的邻接矩阵
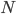
- 添加自回路,得到矩阵
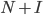
- 循环对
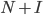 做Expansion和Inflation操作,即计算公式(1)和(2),直到收敛
做Expansion和Inflation操作,即计算公式(1)和(2),直到收敛 - 根据最终得到的矩阵,进行划分聚类
此算法是我在上《生物信息学中的算法设计》课上是学到的,当时觉得这个算法真是神奇,如此简单,但又如此有效,实在高明。查阅文献得知,此为Stijn van Dongen的博士论文,本博客的图片均来自其博士论文,想深入了解图聚类算法,请下载他的论文。


Pingback: hihoCoder 1504-骑士游历 | bitJoy > code