随机矩阵是这样一类方阵，其元素为非负实数，且行和或列和为1。如果行和为1，则称为行随机矩阵；如果列和为1，则称为列随机矩阵；如果行和和列和都为1，则称为双随机矩阵。

前面我们介绍的谷歌矩阵和HMM中的转移矩阵都属于随机矩阵，所以随机矩阵也称为概率矩阵、转移矩阵、或马尔可夫矩阵。

随机矩阵有一个性质，就是其所有特征值的绝对值小于等于1，且其最大特征值为1。下面通过两种方法证明这个结论。

首先，随机矩阵A肯定有特征值1，即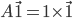$\begin{equation}A\vec 1=1\times\vec 1\end{equation}$其中的单位向量$\vec 1=(\frac{1}{n},...,\frac{1}{n})^T$，因为A的行和为1，所以上述等式成立。即1是A的特征值。

反证法

假设存在大于1的特征值$\lambda$，则有$A\vec x=\lambda\vec x$。令$x_k$是$\vec x$中最大的元素。又因为A的元素非负，且行和为1，所以$\lambda\vec x$中的每个元素都是$\vec x$中元素的凸组合，所以$\lambda\vec x$中的每个元素都小于等于$x_k$。

$\begin{equation}a_{i1}x_1+a_{i2}x_2+...+a_{in}x_n=\lambda x_i\leq x_k\end{equation}$

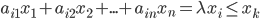
但是如果$\lambda>1$，则$\lambda x_k>x_k$，和(2)式矛盾，所以$\lambda\leq 1$。又因为(1)式，所以A的最大特征值为1。

常规证法

设对称随机矩阵A的特征值$\lambda$对应的特征向量为$x$（为了简便，以下省略向量符号），则有$Ax=\lambda x$，即$x^TAx=\lambda x^Tx$，欲证明$|\lambda|\leq 1$，只需证明

$\begin{equation}\lambda=\frac{<x,Ax>}{<x,x>}\leq 1\end{equation}$

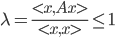
根据定义有：

$\begin{equation}<x,Ax>=\sum_{i=1}^na_{ii}x_i^2+2\sum_{i<j,i\sim j}a_{ij}x_ix_j\end{equation}$

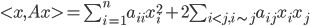
对于$i<j,i\sim j$，有：

$\begin{equation}a_{ij}(x_i-x_j)^2=a_{ij}x_i^2-2a_{ij}x_ix_j+a_{ij}x_j^2\end{equation}$

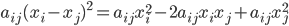
两边求和并移项得到：

$\begin{equation}\begin{array}\displaystyle{2\sum_{i<j}}a_{ij}x_ix_j & = & \displaystyle{\sum_{i<j}a_{ij}x_i^2+\sum_{i<j}a_{ij}x_j^2-\sum_{i<j}a_{ij}(x_i-x_j)^2}\\ & = & \displaystyle{\sum_{i<j}a_{ij}x_i^2+\sum_{i<j}a_{ji}x_j^2-\sum_{i<j}a_{ij}(x_i-x_j)^2}\\ & = & \displaystyle{\sum_{i<j}a_{ij}x_i^2+\sum_{i>j}a_{ij}x_i^2-\sum_{i<j}a_{ij}(x_i-x_j)^2}\\ & = & \displaystyle{\sum_i(\sum_{j\neq i}a_{ij}x_i^2)-\sum_{i<j}a_{ij}(x_i-x_j)^2}\\ & = & \displaystyle{\sum_i(x_i^2(1-a_{ii}))-\sum_{i<j}a_{ij}(x_i-x_j)^2}\end{array}\end{equation}$

第2、3个等号都是因为A是对称矩阵，所以可以把$a_{ij}$替换为$a_{ji}$，然后互换$i,j$下标。最后一个等号是因为A的行和为1。

将(6)代入(4)式得到：

$\begin{equation}\begin{array}\displaystyle{<x,Ax>} & = & \displaystyle{\sum_ia_{ii}x_i^2+\sum_i(x_i^2(1-a_{ii}))-\sum_{i<j}a_{ij}(x_i-x_j)^2}\\ & = & \displaystyle{\sum_ix_i^2-\sum_{i<j}a_{ij}(x_i-x_j)^2}\end{array}\end{equation}$

所以：

$\begin{equation}\lambda=\frac{<x,Ax>}{<x,x>} = \frac{\sum_ix_i^2-\sum_{i<j}a_{ij}(x_i-x_j)^2}{\sum_ix_i^2} \leq 1\end{equation}$

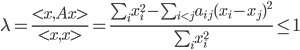
又因为(1)式，所以A的最大特征值为1。

随机矩阵的第二大特征值$\lambda(A)$也很有用，$1-\lambda(A)$被称为矩阵A的谱间隔（spectral gap），它衡量的是最大特征值和第二大特征值之间的差值。$\lambda(A)$在马尔可夫随机游走领域有重要作用。

$\begin{equation}||A^lp-1||_2\leq \lambda^l(A)\end{equation}$

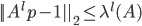
上式是扩张图（Expander）领域很重要的一个引理，A为扩张图的邻接矩阵，$p$为在所有节点上的初始概率分布，$\lambda(A)$为矩阵A的第二大的特征值。因为$\lambda(A)<1$，所以$\lambda^l(A)$会快速的降到0。也就是说，在初始概率$p$上，随机游走$l$步，很快就能达到均匀分布$1$。