上一篇博客主要介绍了逻辑回归的理论知识，这篇博客咱们用Python机器学习包sklearn中的LogisticRegression做一个分类的实例。
数据还是学生样本，只有两个特征，分别是两门课的分数score1和score2，类标号y表示这个学生是否能被录取。先上分类效果图：
逻辑回归之Python应用实例
Leave a reply
Category Archives: 0和1
初探逻辑回归
最近实验室在组织学习NG的机器学习视频，我也跟进了一下。讲到逻辑回归那一课，一直想不明白，逻辑回归到底是怎样分类的？逻辑回归的分类面在哪里？逻辑回归有像SVM的max margin那样清晰的推导过程吗？为什么需要Sigmoid函数？今天就让我们来一窥逻辑回归的始末。
假设有一堆学生样本，为了简单起见，只有两个特征，分别是两门课的分数score1和score2，类标号y表示这个学生是否能被录取。可视化如下图，黑点表示y=1即被录取，红点表示y=0即未被录取，可以看到黑点处在score1和score2都比较高的区域。我们的任务就是给定这些训练样本，需要确定一个分类面来划分这两类数据。
Gperftools性能分析工具使用教程
上一篇博客简单介绍了Linux平台下不同性能分析工具的特点，最后是Google出品的gperftools胜出。今天我们将举一个用gperftools对链接库进行性能分析的例子。
假设我们创建了一个TestGperftools项目，其中包括一个动态链接库模块complex和主程序main，build文件夹用于存放动态链接库和可执行程序，文件结构如下所示。
czl@ubuntu:~/czl/TestGperftools$ tree . ├── build ├── complex │ ├── complex.cpp │ ├── complex.h │ └── Makefile ├── main │ ├── main.cpp │ └── Makefile └── Makefile 3 directories, 6 files
Linux性能分析工具简介
这半年一直在研究pLink 2的加速策略，了解了相关的性能分析工具，现记录如下。
对软件进行加速的技术路线一般为：首先对代码进行性能分析（ performance analysis，也称为 profiling），然后针对性能瓶颈提出优化方案，最后在大数据集上评测加速效果。所以进行性能优化的前提就是准确地测量代码中各个模块的时间消耗。听起来很简单，不就是测量每行代码的运行时间吗，直接用time_t t=clock();不就好了，但是事情并没有那么简单。如果只进行粗粒度的性能分析，比如测量几个大的模块的运行时间，clock()还比较准确，但是如果测量的是运算量比较小的函数调用，而且有大量的小函数调用，clock()就不太准确了。
比如下面的一段代码，我最开始的性能分析方法是在fun1()~fun3()前后添加time_t t=clock()，然后作差求和的。但是3个fun()加起来的时间居然不等于整个while循环的时间，有将近50%的时间不翼而飞了！
while(true) {
if(fun1()) {
for(int i=0;i<k;++k) {
if(flag1) {
fun2();
}
}
} else {
fun3();
}
}
一种可能是while循环以及内部的for循环本身占用了较多的时间，但是好像不太可能呀。还有一种可能是clock()测量有误，time_t只能精确到秒，clock_t只能精确到毫秒，如果一次fun*()的时间太短，导致一次测量几乎为0，那么多次的while和for循环调用累加的时间也几乎为0，导致实际测量到的fun*()时间远小于真实时间。所以自己用代码进行性能分析可能会有较大的误差，最好借助已有的性能分析工具。 Continue reading
C++基本数据类型备忘
今天阅读《C++ Primer, 5e》的第二章，介绍C++的基本内置类型，觉得有一些平时工作容易出错的知识点，现摘录如下：
unsigned char c = -1; // 假设char占8比特，c的值为255
当我们赋给无符号类型一个超出它表示范围的值时，结果是初始值对无符号类型表示数值总数取模后的余数。例如，8比特大小的unsigned char可以表示0至255区间内的值，如果我们赋了一个区间以外的值，则实际的结果是该值对256取模后所得的余数。因此，把-1赋给8比特大小的unsigned char所得的结果是255。
signed char c2 = 256; // 假设char占8比特，c2的值是未定义的
当我们赋给带符号类型一个超出它表示范围的值时，结果是未定义的（undefined）。此时，程序可能继续工作、可能崩溃，也可能生成垃圾数据。 Continue reading
随机矩阵及其特征值
随机矩阵是这样一类方阵，其元素为非负实数，且行和或列和为1。如果行和为1，则称为行随机矩阵；如果列和为1，则称为列随机矩阵；如果行和和列和都为1，则称为双随机矩阵。
前面我们介绍的谷歌矩阵和HMM中的转移矩阵都属于随机矩阵，所以随机矩阵也称为概率矩阵、转移矩阵、或马尔可夫矩阵。
随机矩阵有一个性质，就是其所有特征值的绝对值小于等于1，且其最大特征值为1。下面通过两种方法证明这个结论。
首先，随机矩阵A肯定有特征值1，即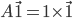
其中的单位向量$\vec 1=(\frac{1}{n},...,\frac{1}{n})^T$，因为A的行和为1，所以上述等式成立。即1是A的特征值。
马尔可夫聚类算法
马尔可夫聚类算法（The Markov Cluster Algorithm, MCL）是一种快速可扩展的基于图的聚类算法。它的基本思想为：在一个稀疏图G中，如果某个区域A是稠密的（是一个聚类），则在A中随机游走k步，还在A内的概率很大，也就是说，A内的k步路径（k-length path）很多。所以我们可以在图中随机游走k步，如果某个区域连通的概率很大，则该区域是一个聚类。随机游走的下一步只和当前所处节点有关，也就是说这是一个马尔可夫的随机游走过程。
我们用一个例子来演示马尔可夫聚类算法的过程。
隐马尔可夫模型及其应用（2）学习问题&识别问题
上一回介绍了HMM的解码问题，今天我们介绍HMM的学习问题和识别问题，先来看学习问题。
正如上一回结束时所说，HMM的学习问题是：仅已知观测序列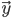
，要估计出模型参数组
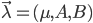，其中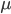
为初始概率分布向量，
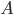为转移概率矩阵，
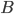为发射概率矩阵。
算法设计
求解HMM的参数学习问题，就是求解如下的最优化问题：
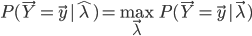
也就是找一个参数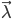
，使得模型在该参数下最有可能产生当前的观测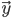。如果使用极大似然法求解，对于似然函数
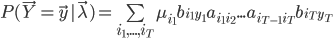而言，这个最大值问题的计算量过大，在实际中是不可能被采用的。为此，人们构造了一个递推算法，使其能相当合理地给出模型参数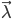的粗略估计。其核心思想是：并不要求备选
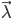使得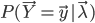
达到最大或局部极大，而只要求使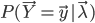相当大，从而使计算变为实际可能。 Continue reading
隐马尔可夫模型及其应用（1）简介&解码问题
隐马尔可夫模型（Hidden Markov Model, HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。
先举一个简单的例子以直观地理解HMM的实质——韦小宝的骰子。
稳定版快速排序算法
我们知道常规的快速排序算法是一个不稳定的算法，也就是两个相等的数排序之后的顺序可能和在原序列中的顺序不同。这是因为当选定一个枢轴（pivot），要把其他数分到小于pivot和大于pivot的两边的时候，不同实现的分法不一样。
下面我实现了一种稳定版快速排序算法，在Partition函数中保持了原序列中所有元素的相对顺序，只把pivot放到了它的正确位置。具体方法是三遍扫描原序列：1）第一遍先把小于pivot的元素按先后顺序放到tmp里，然后把pivot放到它的正确位置tmp[k]；2）第二遍把大于pivot的元素按先后顺序追加在tmp里，这样除了pivot以前的其他元素，都保持了和原序列中一样的顺序；3）第三遍把tmp赋值回原数组A。
当排序算法稳定之后，就可以借此统计逆序数了，文件Q5.txt中共包含100000个不同的整数，每行一个数。我们可以使用稳定版快速排序算法对其排序，并统计出其中的逆序数个数。 Continue reading