由于本书成书较早(2015),作者当时使用的是Theano,但Theano已不再维护,所以本博客使用当下流行的Pytorch框架讲解MNIST图片分类的代码实现,具体就是Pytorch官方给出的MNIST代码:
https://github.com/pytorch/examples/tree/master/mnist。
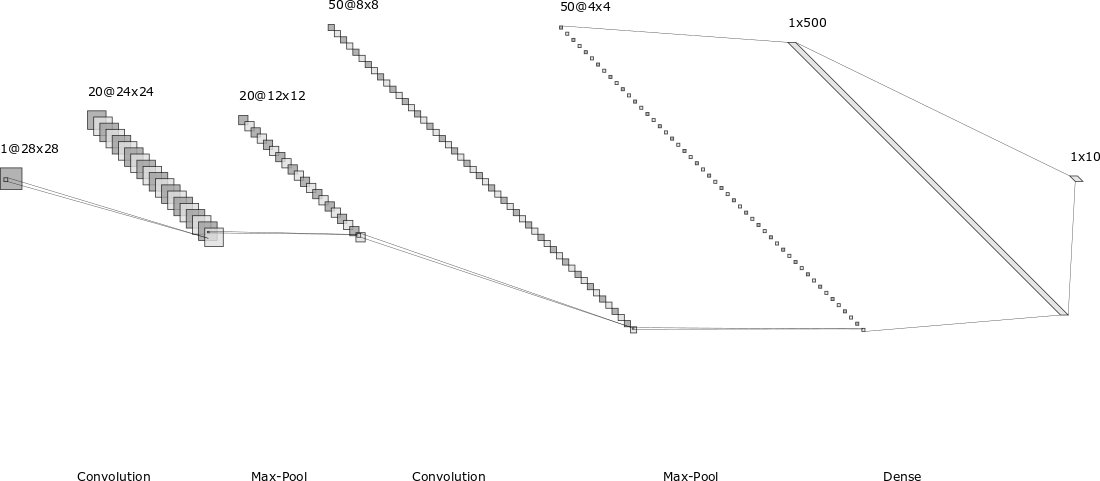
http://alexlenail.me/NN-SVG/LeNet.html
由于本书成书较早(2015),作者当时使用的是Theano,但Theano已不再维护,所以本博客使用当下流行的Pytorch框架讲解MNIST图片分类的代码实现,具体就是Pytorch官方给出的MNIST代码:
https://github.com/pytorch/examples/tree/master/mnist。

今天我们终于进入到了本书的重头戏——深度学习。其实,这一章的深度学习主要介绍的是卷积神经网络,即CNN。
本书之前的章节介绍的都是如下图的全连接网络,虽然全连接网络已经能够在MNIST数据集上取得98%以上的测试准确率,但有两个比较大的缺点:1. 训练参数太多,容易过拟合;2. 难以捕捉图片的局部信息。第一点很好理解,参数一多,网络就难以训练,难以加深。对于第二点,因为全连接的每个神经元都和上一层的所有神经元相连,无论距离远近,也就是说网络不会捕捉图片的局部信息和空间结构信息。

本章我们将分析一下为什么深度神经网络难以训练的问题。
首先来看问题:如果神经网络的层次不断加深,则在BP误差反向传播的过程中,网络前几层的梯度更新会非常慢,导致前几层的权重无法学习到比较好的值,这就是梯度消失问题(The vanishing gradient problem)。
以我们在第三章学习的network2.py为例(交叉熵损失函数+Sigmoid激活函数),我们可以计算每个神经元中误差对偏移量$b$的偏导$\partial C/ \partial b$,根据第二章BP网络的知识,$\partial C/ \partial b$也是$\partial C/ \partial w$的一部分(BP3和BP4的关系),所以如果$\partial C/ \partial b$的绝对值大,则说明梯度大,在误差反向传播的时候,$b$和$w$更新就快。

我们应该都听说过神经网络强大到能拟合任意一个函数,但细究起来很少有人能论证这个观点,这一章就用通俗易懂的图解方式来证明神经网络为什么能拟合任意一个函数。
开始介绍之前,有两点需要注意:
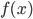 ,而是说当隐藏层神经元增加时,可以无限逼近
,而是说当隐藏层神经元增加时,可以无限逼近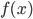 ,比如对于任何一个输入
,比如对于任何一个输入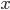 ,网络的输出
,网络的输出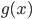 和正确值
和正确值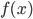 的差小于某个阈值,
的差小于某个阈值,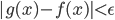 ;
;假设给定一个下图的连续函数,函数形式未知,本章将用图解的方式来证明,一个单隐层的神经网络就可以很好的拟合这个未知函数。
权重初始化
在之前的章节中,我们都是用一个标准正态分布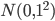 初始化所有的参数
初始化所有的参数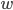 和
和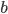 ,但是当神经元数量比较多时,会出现意想不到的问题。
,但是当神经元数量比较多时,会出现意想不到的问题。
假设一个神经网络的输入层有1000个神经元,且某个样本的1000维输入中,恰好有500维是0,另500维是1。我们目前考察隐藏层的第一个神经元,则该神经元为激活的输出为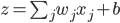 ,因为输入中的500维是0,所以
,因为输入中的500维是0,所以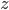 相当于有501个来自
相当于有501个来自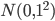 的随机变量相加。因为
的随机变量相加。因为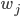 和
和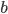 的初始化都是独立同分布的,所以
的初始化都是独立同分布的,所以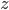 也是一个正态分布,均值为0,但方差变成了
也是一个正态分布,均值为0,但方差变成了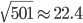 ,即
,即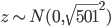 。我们知道对于正态分布,如果方差越小,则分布的形状是高廋型的;如果方差越大,则分布的形状是矮胖型的。所以
。我们知道对于正态分布,如果方差越小,则分布的形状是高廋型的;如果方差越大,则分布的形状是矮胖型的。所以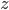 有很大的概率取值会远大于1或远小于-1。又因为激活函数是sigmoid,当
有很大的概率取值会远大于1或远小于-1。又因为激活函数是sigmoid,当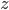 远大于1或远小于-1时,
远大于1或远小于-1时,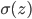 趋近于1或者0,且导数趋于0,变化缓慢,导致梯度消失。
趋近于1或者0,且导数趋于0,变化缓慢,导致梯度消失。
首先介绍一下神经网络中不同数据集的功能,包括训练集、验证集和测试集。
训练集是用来训练网络参数的。当觉得在训练集上训练得差不多时,就可以在验证集上进行测试,如果验证集上的性能不好,则需要调整网络结构或者超参数,重新在训练集上训练。所以本质上验证集指导训练过程,也参与了训练和调参。为了防止网络对验证集过拟合,当网络在训练集和验证集上表现都不错时,就可以在测试集上进行测试了。测试集上的性能代表了模型的最终性能。
当然如果发现网络在测试集上性能不好,可能还会反过来去优化网络,重新训练和验证,这么说测试集最终也变相参与了调优。如果一直这么推下去的话,就没完没了了,所以一般还是认为用验证集对模型进行优化,用测试集对模型性能进行测试。
过拟合的含义就是网络在训练集上性能很好,但是在验证集(或者测试集)上的性能较差,这说明网络在训练集上训练过头了,对训练集产生了过拟合。为了便于叙述,本文没有验证集,直接使用测试集作为验证集对模型进行调优,所以主要考察网络在训练集和测试集上的性能表现。
Continue reading原文的第三章内容较多,本博客将分三个部分进行介绍:梯度消失、过拟合与正则化、权重初始化及其他,首先介绍梯度消失问题。
为简单起见,假设网络只包含一个输入和一个神经元,网络的损失是均方误差损失MSE,激活函数是Sigmoid函数。则该网络的参数只包含权重$w$和偏移量$b$。我们想训练这个网络,使得当输入为1时,输出0。

这一讲介绍误差反向传播(backpropagation)网络,简称BP网络。
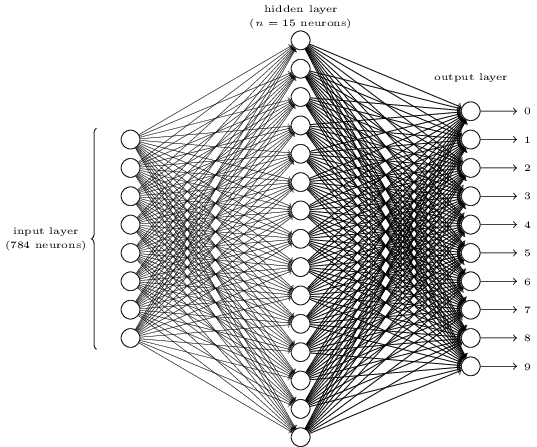
以上一讲介绍的MNIST手写数字图片分类问题为研究对象,首先明确输入输出:输入就是一张28×28的手写数字图片,展开后可以表示成一个长度为784的向量;输出可以表示为一个长度为10的one-hot向量,比如输入是一张“3”的图片,则输出向量为(0,0,0,1,0,0,0,0,0,0,0)。
然后构造一个如下的三层全连接网络。第一层为输入层,包含784个神经元,正好对应输入的一张28×28的图片。第二层为隐藏层,假设隐藏层有15个神经元。第三层为输出层,正好10个神经元,对应该图片的one-hot结果。
全连接网络表示上一层的每个神经元都和下一层的每个神经元有连接,即每个神经元的输入来自上一层所有神经元的输出,每个神经元的输出连接到下一层的所有神经元。每条连边上都有一个权重w。
最近开始学习神经网络和深度学习,使用的是网上教程:http://neuralnetworksanddeeplearning.com/,这是学习心得第一讲,介绍经典的MNIST手写数字图片数据集。
MNIST(Modified National Institute of Standards and Technology database)数据集改编自美国国家标准与技术研究所收集的更大的NIST数据集,该数据集来自250个不同人手写的数字图片,一半是人口普查局的工作人员,一半是高中生。该数据集包括60000张训练集图片和10000张测试集图片,训练集和测试集都提供了正确答案。每张图片都是28×28=784大小的灰度图片,也就是一个28×28的矩阵,里面每个值是一个像素点,值在[0,1]之间,0表示白色,1表示黑色,(0,1)之间表示不同的灰度。下面是该数据集中的一些手写数字图片,可以有一个感性的认识。