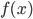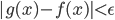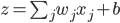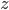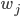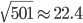今天开始介绍大名鼎鼎的NLP网课Stanford-CS224N。第一讲内容为课程简介和词向量。
词向量即用来表示这个词的含义的向量。早期的NLP常用one-hot编码来表示词向量，假如词典中共有10000个词，则这个one-hot向量长度就是10000，该词在词典中所处位置对应的值为1，其他值为0。
one-hot表示方法虽然简单，但其有诸多缺点：1. 词典中的词是不断增多的，比如英语，通过对原有的词增加前缀和后缀，可以变换出很多不同的词，one-hot编码会导致向量维度非常大，且每个向量是稀疏的；2. 不同词的one-hot编码向量是垂直的，在向量空间中无法表示近似关系，即使两个含义相近的词，它们的词向量点积也为0。
既然one-hot编码有这么多缺点，那我们就换一种编码，one-hot是高维稀疏向量，那新的编码就改用低维稠密向量，这样就解决了上述问题，那么怎样得到一个词的低维稠密的词向量呢？这就是word2vec算法。
Continue reading相信很多学CS的同学之前都没听说过“蛋白质结构预测”这个问题，直到2018年12月初，一则劲爆消息瞬间引爆了CSer的朋友圈，那就是Google Deepmind团队开发的AlphaFold一举拿下当年的CASP比赛冠军，而且远远甩开了第二名。我当时就转载过类似的公众号文章，大家可以阅读并想象当时朋友圈的欢呼声：阿尔法狗再下一城 | 蛋白结构预测AlphaFold大胜传统人类模型。
当时，很多同学也转载过类似的文章，但其实很少有人真正明白“蛋白质结构预测”这个问题是什么，它的难度有多大，CASP是个什么比赛，以及AlphaFold的内部原理是什么。当然，对于这一连串的问题，我当时也是懵逼的。不过自己好歹也是个跟蛋白质有关的PhD，如此热点事件，自然是要关注的。不过之后一直没时间，直到今年相关顶级文章再次爆出，我就借着准备文献讲评的机会了解了相关的知识，在这里跟大家分享一下。
由于本书成书较早（2015），作者当时使用的是Theano，但Theano已不再维护，所以本博客使用当下流行的Pytorch框架讲解MNIST图片分类的代码实现，具体就是Pytorch官方给出的MNIST代码：
https://github.com/pytorch/examples/tree/master/mnist。
简化版：
今天我们终于进入到了本书的重头戏——深度学习。其实，这一章的深度学习主要介绍的是卷积神经网络，即CNN。
本书之前的章节介绍的都是如下图的全连接网络，虽然全连接网络已经能够在MNIST数据集上取得98%以上的测试准确率，但有两个比较大的缺点：1. 训练参数太多，容易过拟合；2. 难以捕捉图片的局部信息。第一点很好理解，参数一多，网络就难以训练，难以加深。对于第二点，因为全连接的每个神经元都和上一层的所有神经元相连，无论距离远近，也就是说网络不会捕捉图片的局部信息和空间结构信息。
本章我们将分析一下为什么深度神经网络难以训练的问题。
首先来看问题：如果神经网络的层次不断加深，则在BP误差反向传播的过程中，网络前几层的梯度更新会非常慢，导致前几层的权重无法学习到比较好的值，这就是梯度消失问题（The vanishing gradient problem）。
以我们在第三章学习的network2.py为例（交叉熵损失函数+Sigmoid激活函数），我们可以计算每个神经元中误差对偏移量$b$的偏导$\partial C/ \partial b$，根据第二章BP网络的知识，$\partial C/ \partial b$也是$\partial C/ \partial w$的一部分（BP3和BP4的关系），所以如果$\partial C/ \partial b$的绝对值大，则说明梯度大，在误差反向传播的时候，$b$和$w$更新就快。
我们应该都听说过神经网络强大到能拟合任意一个函数，但细究起来很少有人能论证这个观点，这一章就用通俗易懂的图解方式来证明神经网络为什么能拟合任意一个函数。
开始介绍之前，有两点需要注意：
，而是说当隐藏层神经元增加时，可以无限逼近，比如对于任何一个输入
，网络的输出
和正确值的差小于某个阈值，
；假设给定一个下图的连续函数，函数形式未知，本章将用图解的方式来证明，一个单隐层的神经网络就可以很好的拟合这个未知函数。
权重初始化
在之前的章节中，我们都是用一个标准正态分布
初始化所有的参数
和
，但是当神经元数量比较多时，会出现意想不到的问题。
假设一个神经网络的输入层有1000个神经元，且某个样本的1000维输入中，恰好有500维是0，另500维是1。我们目前考察隐藏层的第一个神经元，则该神经元为激活的输出为
，因为输入中的500维是0，所以
相当于有501个来自的随机变量相加。因为
和的初始化都是独立同分布的，所以也是一个正态分布，均值为0，但方差变成了
，即
。我们知道对于正态分布，如果方差越小，则分布的形状是高廋型的；如果方差越大，则分布的形状是矮胖型的。所以有很大的概率取值会远大于1或远小于-1。又因为激活函数是sigmoid，当远大于1或远小于-1时，
趋近于1或者0，且导数趋于0，变化缓慢，导致梯度消失。
首先介绍一下神经网络中不同数据集的功能，包括训练集、验证集和测试集。
训练集是用来训练网络参数的。当觉得在训练集上训练得差不多时，就可以在验证集上进行测试，如果验证集上的性能不好，则需要调整网络结构或者超参数，重新在训练集上训练。所以本质上验证集指导训练过程，也参与了训练和调参。为了防止网络对验证集过拟合，当网络在训练集和验证集上表现都不错时，就可以在测试集上进行测试了。测试集上的性能代表了模型的最终性能。
当然如果发现网络在测试集上性能不好，可能还会反过来去优化网络，重新训练和验证，这么说测试集最终也变相参与了调优。如果一直这么推下去的话，就没完没了了，所以一般还是认为用验证集对模型进行优化，用测试集对模型性能进行测试。
过拟合的含义就是网络在训练集上性能很好，但是在验证集（或者测试集）上的性能较差，这说明网络在训练集上训练过头了，对训练集产生了过拟合。为了便于叙述，本文没有验证集，直接使用测试集作为验证集对模型进行调优，所以主要考察网络在训练集和测试集上的性能表现。
Continue reading原文的第三章内容较多，本博客将分三个部分进行介绍：梯度消失、过拟合与正则化、权重初始化及其他，首先介绍梯度消失问题。
为简单起见，假设网络只包含一个输入和一个神经元，网络的损失是均方误差损失MSE，激活函数是Sigmoid函数。则该网络的参数只包含权重$w$和偏移量$b$。我们想训练这个网络，使得当输入为1时，输出0。
