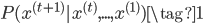今天要介绍的内容比较多,但都是概述性的内容,主要了解自然语言生成领域的进展。
Section 1: Recap LMs and decoding algorithms
之前已经讲过什么是语言模型,语言模型就是给定句子中的一部分词,要求预测下一个词是什么。形式化表述就是预测$P(y_t|y_1,...,y_{t-1})$,其中的$y_1,...,y_{t-1}$就是目前已知的词,$y_t$就是要预测的下一个词。
条件语言模型是指除了已知$y_1,...,y_{t-1}$,还给定了$x$,这个$x$就是提供给语言模型的额外的信息。比如机器翻译的$x$就是源语言的句子信息;自动摘要的$x$就是输入的长文;对话系统的$x$就是历史对话内容等。
需要提醒的是,语言模型在训练阶段,输入Decoder的是正确的词,这种方法被称为Teacher Forcing,即不论上一步的输出是什么,都强制给这一步输入正确的词。而如果在测试阶段,Decoder的输入是上一步的输出。