每年春晚过后,央视又要吹嘘说今年春晚收视率创新高了,但是我们总感觉央视在骗我们,因为我是越长大越不看春晚了[笑cry],所以收视率到底是怎么统计出来的,央视的说法是否靠谱呢?
最近的美国大选真是热闹,很多机构都会发放一些调查问卷,然后统计出希拉里或者唐纳德的民众支持率是多少,但是我并没有收到调查问卷,凭什么就得出了民众支持率了,意思是把我排除在民众之外咯?所以引出这样一个问题,调查问卷是否可信,即调查问卷的有效性。

其实,央视统计收视率并不要问全中国14亿人口有多少人看了春晚,他只需要从14亿人口里面随机抽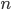 个人,问一下这
个人,问一下这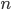 个人里有多少人看了春晚,然后把看的人数除以总数就大概估计出全国的收视率了。同理调查民众支持率也是一样,只需要随机调查
个人里有多少人看了春晚,然后把看的人数除以总数就大概估计出全国的收视率了。同理调查民众支持率也是一样,只需要随机调查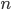 个人的意向,把支持希拉里的人数除以总数就大概得到了希拉里的支持率。
个人的意向,把支持希拉里的人数除以总数就大概得到了希拉里的支持率。
但是你要问了,通过抽样调查出来的收视率和支持率靠谱吗,需要随机抽样多少人才能得到一个比较好的全局近似解呢?今天我们就来解决这个问题。
假设我们随机抽样了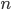 个人,分别是
个人,分别是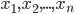 。如果第
。如果第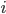 个人看了春晚,则
个人看了春晚,则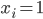 ,否则
,否则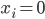 。那么通过这
。那么通过这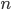 个人的收视情况,我们可以估计出一个收视率
个人的收视情况,我们可以估计出一个收视率
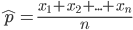
假设全国的真实收视率是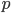 ,那么平均到每一个人,他看了春晚的概率就是
,那么平均到每一个人,他看了春晚的概率就是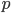 ,也即
,也即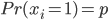 ,所以有
,所以有
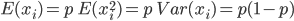
我们的目的就是希望通过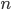 个人估计出来的
个人估计出来的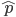 和
和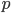 越接近越好。换句话说,我们希望
越接近越好。换句话说,我们希望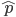 和
和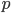 相差大于5%的概率要小于5%。再换句话说就是有至少95%的概率,
相差大于5%的概率要小于5%。再换句话说就是有至少95%的概率,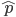 和
和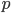 相差在5%以内,即
相差在5%以内,即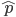 和
和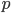 很接近。注意这里的两个5%都是可以换成任意你想要的精度。用数学语言表示就是,
很接近。注意这里的两个5%都是可以换成任意你想要的精度。用数学语言表示就是,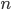 至少为多少时,以下不等式可以被满足。
至少为多少时,以下不等式可以被满足。
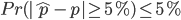
把(1)式代入(3)式,用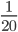 代替5%,得到等价形式:
代替5%,得到等价形式:
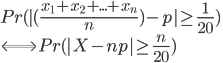
其中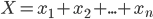 。根据期望的线性可加性,有
。根据期望的线性可加性,有
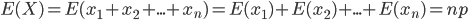
所以(4)又等价于
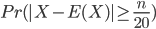
我们需要利用著名的切比雪夫不等式来求解上式,切比雪夫不等式如下:
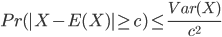
切比雪夫不等式可以直接由马尔可夫不等式得到,马尔可夫不等式的证明也不难,略过。
利用切比雪夫不等式求解(6)式
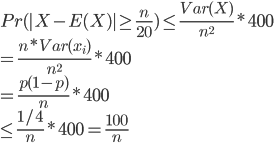
第一个等号是因为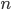 个变量是独立同分布的,所以方差也有类似于(5)式的线性性质。最后一个不等号是因为
个变量是独立同分布的,所以方差也有类似于(5)式的线性性质。最后一个不等号是因为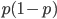 是一个开口向下的抛物线,在
是一个开口向下的抛物线,在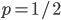 时取到极值
时取到极值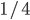 。
。
回到最初的不等式(3),则(8)式要满足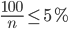 ,解得
,解得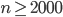 。注意到求出的
。注意到求出的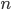 和总体人数是无关的,也就是说,虽然全中国有十几亿人口,但是央视只要随机抽样调查2000个人的收视情况,就能以比较高的概率准确估计出全国的收视率。
和总体人数是无关的,也就是说,虽然全中国有十几亿人口,但是央视只要随机抽样调查2000个人的收视情况,就能以比较高的概率准确估计出全国的收视率。
这个结论还是很漂亮的,但是这种方法有两个限制条件:
- 采样满足独立同分布,即这
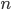 个人是独立同分布的,不能针对某一特定人群调查
个人是独立同分布的,不能针对某一特定人群调查 - (3)式的5%是一个绝对误差,当
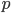 本身很小的时候,容易被5%淹没
本身很小的时候,容易被5%淹没
对于第1个问题,稍微好处理一点,抽样的时候尽量随机一点。对于第2个问题,比较好的解决办法是引入相对误差,即把(3)式转换为如下的不等式
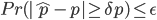
(9)式的求解就比较复杂了,得出的结论也没有上面那么简单,具体的求解方法请听下回分解。
Pingback: 调查问卷的有效性(2)相对误差 | bitJoy