这一讲介绍误差反向传播(backpropagation)网络,简称BP网络。
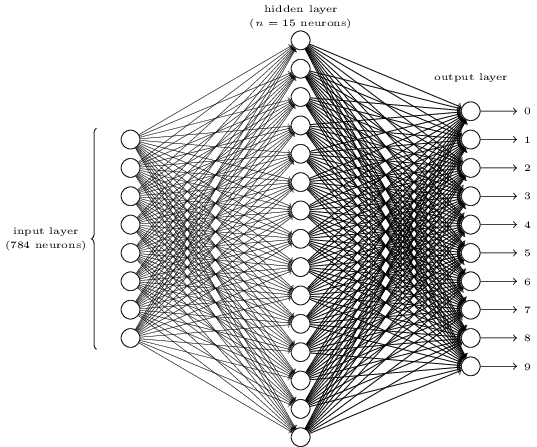
以上一讲介绍的MNIST手写数字图片分类问题为研究对象,首先明确输入输出:输入就是一张28×28的手写数字图片,展开后可以表示成一个长度为784的向量;输出可以表示为一个长度为10的one-hot向量,比如输入是一张“3”的图片,则输出向量为(0,0,0,1,0,0,0,0,0,0,0)。
然后构造一个如下的三层全连接网络。第一层为输入层,包含784个神经元,正好对应输入的一张28×28的图片。第二层为隐藏层,假设隐藏层有15个神经元。第三层为输出层,正好10个神经元,对应该图片的one-hot结果。
全连接网络表示上一层的每个神经元都和下一层的每个神经元有连接,即每个神经元的输入来自上一层所有神经元的输出,每个神经元的输出连接到下一层的所有神经元。每条连边上都有一个权重w。
每个神经元执行的操作非常简单,就是把跟它连接的每个输入乘以边上的权重,然后累加起来。
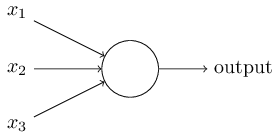
比如上面的一个神经元,它的输出就是:
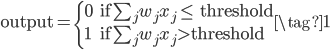
其中的threshold就是该神经元激活的阈值,如果累加值超过threshold,则该神经元被激活,输出为1,否则为0。这就是最原始的感知机网络。感知机网络也可以写成如下的向量形式,用激活阈值b代替threshold,然后移到左边。神经网络中,每条边具有权重w,每个神经元具有激活阈值b。
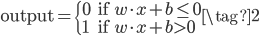
但是感知机网络的这种激活方式不够灵活,它在threshold左右有一个突变,如果输入或者某个边上的权重稍微有一点变化,输出结果可能就千差万别了。于是后来人们提出了用sigmoid函数来当激活函数,它在0附近的斜率较大,在两边的斜率较小,能达到和阶梯函数类似的效果,而且函数光滑可导。sigmoid的函数形式如下,其中$z\equiv w \cdot x + b$为神经元激活之前的值。
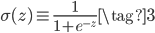
sigmmoid函数还有一个优点就是它的导数很好计算,可以用它本身来表示:
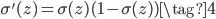
BP网络的参数就是所有连线上的权重w和所有神经元中的激活阈值b,如果知道这些参数,给定一个输入x,则可以很容易的通过正向传播(feedforward)的方法计算到输出,即不断的执行$w \cdot x + b$操作,然后用sigmoid激活,再把上一层的输出传递给下一层作为输入,直到最后一层。
def feedforward(self, a): """Return the output of the network if ``a`` is input.""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a
同时,网络的误差可以用均方误差(mean squared error, MSE)表示,即网络在最后一层的激活值(即网络的输出值)$a$和对应训练集输入$x$的正确答案$y(x)$的差的平方。有$n$个输入则误差取平均,$\dfrac{1}{2}$是为了后续求导方便。
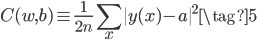
训练BP网络的过程就是不断调整参数——权重weights和阈值biases——使得网络的误差$C$最小。使用的方法是梯度下降,即误差$C$对每个参数求偏导(梯度),然后参数向梯度的反方向更新,这样更新能保证误差$C$下降得最快,至于为什么下降最快,直观上很好理解,数学证明可以看原文,证明也很好理解,而且我认为很精彩。
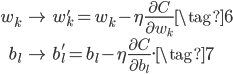
下面我们就来求解梯度下降中最重要的梯度,即$C$对每个参数$w$和$b$的偏导,先正式定义一些记号。
创建网络时,可以对w和b进行随机初始化,代码如下。如果以本文开头的网络结构为例,用[748, 15, 10]输入到下面函数,随机初始化b和w。[748, 15, 10]分别表示第一、二、三层的神经元个数为748,15和10。
def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]
请注意第一层(输入层)神经元是没有阈值b的,所以biases列表只有两项,第一项为15×1的列向量,表示中间层的阈值;第二项为10×1的列向量,表示输出层的阈值。在网络中用$b^l_j$表示第$l$层的第$j$个神经元的阈值,如下$b_3^2$表示第2层的第3个神经元的阈值。

权重由于关系到两层之间,所以本文的三层网络的weights列表也只有两项,第一项为15×748的矩阵,表示中间层和输入层的权重矩阵;第二项为10×15的矩阵,表示输出层和中间层的权重矩阵。在网络中用$w_{jk}^l$表示第$l-1$层的第$k$个神经元和第$l$层的第$j$个神经元的连接权重,这种表示方法和常规的顺序下标表示相反,但是在矩阵相乘时$z^l=w^la^{l-1}+b^l$(下方公式10),不用转置,更方便。

类似的,我们再定义一个神经元激活之前的值为$z$,激活之后的值为$a=\sigma(z)$,上下标的表示方法和$b$的表示方法是一样的。具体来说,
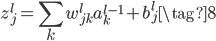
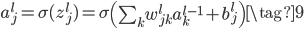
向量形式为:
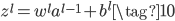
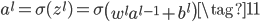
对于输入层神经元来说,输入就等于输出,没有激活一说,所以$a^1=x$。对于单个输入样本$x$来说,网络的误差如下,$L$表示网络的总层数,所以$a^L$表示网络最终的输出。
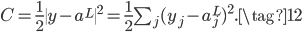
我们的目标就是求出$C$对每个参数的梯度。
首先,引入一个很重要的中间量$\delta^l_j$,表示误差$C$对第$l$层的第$j$个神经元的未激活值$z^l_j$的偏导:
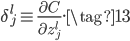
根据定义,对于输出层(假设共有$L$层),使用链式法则和公式(9),有下面的等式。

上式$\frac{\partial C}{\partial a^L_j}$就是损失$C$对最后一层输出$a^L$的偏导,可以用$\nabla_a C$表示。输出层的$\delta^L_j$只和损失以及输出层激活前后的值有关。整体用向量表示为:
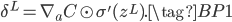
其中的$\odot$表示哈达玛乘积(Hadamard product),就是向量或矩阵的对应位相乘,比如$(s \odot t)_j = s_j t_j$,或:
![\begin{eqnarray}\left[\begin{array}{c} 1 \\ 2 \end{array}\right] \odot \left[\begin{array}{c} 3 \\ 4\end{array} \right]= \left[ \begin{array}{c} 1 * 3 \\ 2 * 4 \end{array} \right]= \left[ \begin{array}{c} 3 \\ 8 \end{array} \right].\tag{15}\end{eqnarray}](http://bitjoy.net/wp-content/plugins/latex/cache/tex_6d687ae377a19f2db25ab6decd5f3604.gif)
如果不是最后一层,则使用链式法则有:

又因为
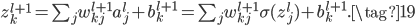
所以
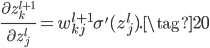
将(20)代入(18)得到:
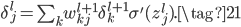
写成向量形式就是:
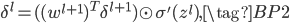
从(BP2)可知,中间层的$\delta^l$可通过下一层的$\delta^{l+1}$递推计算得到。这正体现了误差反向传播的思想,即误差从输出层反向一层一层传到输入层,所以正好可以通过(BP1)和(BP2)计算到所有层的$\delta^l$。
我们推导(BP1)和(BP2)是为了便于求解$C$对$w$和$b$的梯度,进而可以根据公式(6)和(7)更新参数。首先求解$C$对$b$的梯度:
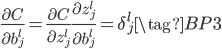
上式中间使用链式法则,中间左式正好是$\delta^l_j$的定义(13),中间右式根据(8)可知等于1,所以误差$C$对神经元阈值$b^l_j$的梯度正好等于$ \delta^l_j$。然后求解$C$对$w$的梯度:
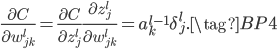
同样利用链式法则和(13)、(8)很容易就能得到上式。可以看到,借助中间量$\delta^l_j$,$C$对$w$和$b$的梯度能很简洁清晰的表示出来,这就是为什么一开始要推导$\delta^l_j$的原因。
以上我们就求到了误差$C$对所有参数的梯度。总结一下就是:

所以,对于单个输入样本$x$,网络的损失对所有参数的偏导可以用如下算法求解:

在真实场景中,样本数往往很多,如果一个样本更新一次参数,则效率比较低,目前通常将一小批样本(batch)一起算一个累加的梯度,然后更新一次,这个过程称为一次迭代(iteration)。当所有样本都迭代过之后,称为一次epoch。下面是针对一次iteration的BP算法,其中的$\eta$为学习率,通俗理解为往梯度下降的方向走多远,$\eta$太大可能引起震荡无法收敛,$\eta$太小训练又太慢,所以需要人工调参。

在BP算法的4个公式中,最重要的是(BP1),因为(BP1)计算了误差开始传播的初始值。(BP1)中的两个分量$\nabla_a C$和$\sigma'(z^L)$又和网络的设计有关。如果使用的损失是均方误差损失(12),使用的激活函数是sigmoid函数(3),则(BP1)可具体写成下面的等式,所以BP算法的4个公式中,所有变量都是已知的了。
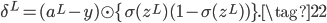
了解了BP的原理之后,代码就非常好理解了,具体可以看GitHub项目,删掉所有注释,真正的核心代码只有74行。使用[784, 30, 10]作为输入,即三层网络,每层神经元个数分别为784,30和10,调用如下代码(表示训练30个epochs,每个batch有10个样本,学习率为3.0),网络在测试集上的分类准确率能达到95%以上。
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
sigmoid函数已经不常用了,现在是relu或者LeakyRelu
是因为sigmoid的梯度消失吗?不过无论用什么激活函数,只要把(BP1)和(BP2)中的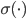 函数的导数换掉就好。
函数的导数换掉就好。
是的,首先是解决梯度消失问题,第二是能更快速收敛,而且不用复杂的计算。导数换掉是自然,只是这个领域发展太快,有的东西已经不再用了。
是的,领域发展太快了,所以作为入门的话,先从基础的、经典的学起比较合适。后续计划更新一些领域内的最新进展,欢迎交流。
Pingback: Neural Networks and Deep Learning(三·一)梯度消失 | bitJoy
Pingback: Neural Networks and Deep Learning(七)番外篇·Pytorch MNIST教程 | bitJoy
Pingback: CS224N(1.15 & 1.17)Backpropagation | bitJoy
Pingback: CS224N(1.24)Language Models and RNNs | bitJoy
Pingback: Neural Networks and Deep Learning(三·一)梯度消失 | bitJoy