$$\begin{equation}Pr(|\hat{p}-p|\geq 5\%)\leq 5\%\end{equation}$$

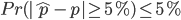
上一回我们讲到当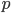$p$本身很小的时候，容易被5%（绝对误差）给淹没掉，导致结果的不可信。我们可以引入相对误差，把(1)式转换为如下的不等式

$$\begin{equation}Pr(|\hat{p}-p|\geq\delta p)\leq\epsilon\end{equation}$$

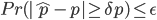
同理，我们可以用

$$\begin{equation}\hat{p}=\frac{x_1+x_2+...+x_n}{n}\end{equation}$$

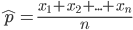
代替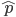$\hat{p}$（建议先看上一篇博客），转换为

$$\begin{equation}Pr(|X-np|\geq\delta np)\end{equation}$$

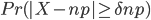
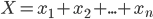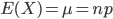类似的，$X=x_1+x_2+...+x_n$，$E(X)=\mu=np$，所以(4)式等价为

$$\begin{equation}Pr(|X-\mu|\geq\delta\mu)\end{equation}$$

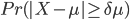
这个时候，因为不等号右边和均值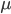$\mu$有关，不能再用切比雪夫不等式了，我们需要另外一个武器：Chernoff bound。它有两种形式：

$$\begin{equation}Pr(X\geq (1+\delta)\mu)\leq[\frac{e^\delta}{(1+\delta)^{1+\delta}}]^\mu\leq e^{-\frac{\mu}{3}\delta^2}\quad\forall\delta>0\end{equation}$$

$$\begin{equation}Pr(X\leq (1-\delta)\mu)\leq[\frac{e^{-\delta}}{(1-\delta)^{1-\delta}}]^\mu\leq e^{-\frac{\mu}{2}\delta^2}\quad\forall 0<\delta<1\end{equation}$$

Chernoff bound的证明需要用到马尔可夫不等式，有一点技巧。以上两种形式可以统一成

$$\begin{equation}Pr(|X-\mu|\geq\delta\mu)\leq 2e^{-\frac{\mu}{3}\delta^2}\end{equation}$$

也是一个很漂亮的不等式。

利用Chernoff bound求解(5)式：

$$\begin{equation}Pr(|X-\mu|\geq\delta\mu)\leq 2e^{-\frac{\mu}{3}\delta^2}\\=2e^{-\frac{np}{3}\delta^2}\leq\epsilon\end{equation}$$

解得

$$\begin{equation}n\geq\left\lceil\frac{3ln\frac{2}{\epsilon}}{p\delta^2}\right\rceil\end{equation}$$

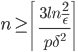
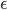这个结果看起来就很复杂了。也就是说，如果要设计调查问卷使满足(2)式的精度，抽样的样本数必须满足(10)式。从(10)式可知，当要求的精度越高（即$\delta$和$\epsilon$越小），所需的样本数越大。并且结果还和真实值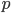$p$有关。