之前写了七篇博客详细介绍了搜索引擎的工作原理。彼时的搜索引擎主要讲查询和网页的相关性匹配,是动态的、在线的、实时的。相关性匹配有一个问题,网页很容易作弊,比如可以在一个网页中写满诸如“免费”、“美容”之类的垃圾关键词,进而提升查询相关性。但是用户在查询时,一定希望返回的网页比较权威可信,比如同样搜索“苹果电脑”,排名第一的应该是Apple的官网,而不应该是中关村在线之类的第三方网站。
权威性是一个静态的(或者说变化较慢的)衡量网页重要性的指标。但是应该怎样度量权威性呢,HITS算法使用authority来度量,即指向自身的网页数量越多,则自身的authority值越大。谷歌的PageRank算法是用PageRank值来衡量权威性的。HITS和PageRank一个比较大的区别是HITS和查询有关,而PageRank和查询无关,所以PageRank可以离线计算。下面主要介绍PageRank算法。

PageRank’s thesis is that a webpage is important if it is pointed to by other important pages.
我先不加解释的给出PageRank的公式,然后带领大家一步步推导出这个公式。
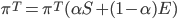
我们首先明确目标:PageRank计算的是网页的静态权威度(PR值),也就是如果给定了一个网络结构,则每个网页的PR值就可以通过PageRank算法计算出。假设网页$P_i$的PR值为$r(P_i)$,则$r(P_i)$等于所有指向$P_i$的网页的PR值之和,即
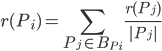
其中$B_{P_i}$为指向$P_i$的网页集合,$|P_j|$为$P_j$的出边的数量。这个式子很好理解,包括两方面内容:1)$\sum\limits_{P_j\in B_{P_i}}$表示如果指向$P_i$的网页数量越多,说明网页$P_i$越重要;2)$\frac{r(P_j)}{|P_j|}$表示如果$P_j$指向的页面数量越少,但有一个指向了$P_i$,说明网页$P_i$越重要(如果一个大牛写了很多推荐信($|P_j|$大),则这些推荐信的效力就下降了,如果大牛只给你写了推荐信($|P_j|=1$),则这封推荐信的效力一定很高)。
(1)式有一个问题,初始给定一个网络结构时,并不知道$r(P_i), r(P_j)$,如何计算呢?Brin和Page利用递归的思想求解,初始假设所有网页的PR值相等,都为$\frac{1}{n}$,其中$n$为网络中网页的数量。则第$k+1$轮的PR计算公式为:
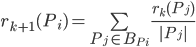
初始对所有网页$P_i$有$r_0(P_i)=\frac{1}{n}$,迭代$k$步之后,可以计算出所有网页的PR值,然后按PR值从大到小排序,就可以知道每个网页的重要性了。
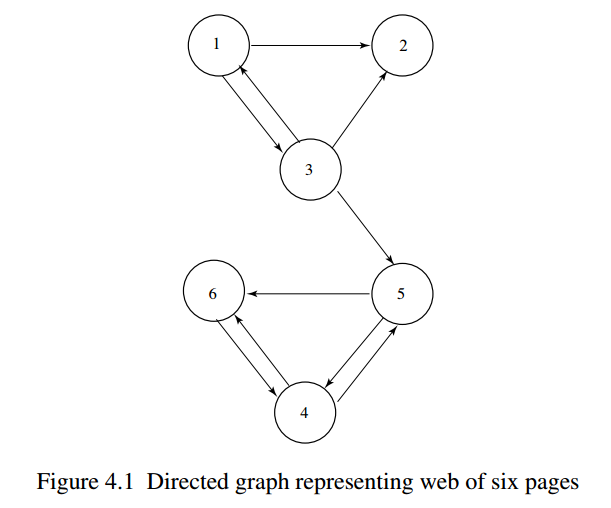
对于上图的小网络,我们可以计算出其每一步的PR值:
可以看到经过2次迭代之后,节点4的PR值最大,从图中也可以看出,节点4的出入边较多,它可能比较重要。
注意到对于(2)式,当$i,j$之间有边时,$\frac{1}{|P_j|}$相当于对$P_j$出度的归一化,设矩阵$H$为图的邻接矩阵的行归一化矩阵,对于上图,为
设行向量$\pi^{(k)T}$为第$k$轮迭代时所有网页的PR值,则式(2)可以转换为如下的矩阵形式:
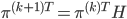
初始有$\pi^{(0)T}=\frac{1}{n}e^T$,$e^T$为全1的行向量。我们可以从(3)式观测出几点信息:
- (3)式的每一轮计算涉及到向量和矩阵的乘法,复杂度为$O(n^2)$,$n$为矩阵$H$的大小
- $H$是一个稀疏矩阵,因为大部分网页只和很少的网页有链接关系,所以上述向量和矩阵的乘法复杂度还可以降低
- $H$有点像马尔科夫链中的随机转移矩阵,但又不完全是,因为如果有dangling nodes,则这一行就是全0,所以$H$被称为substochastic matrix
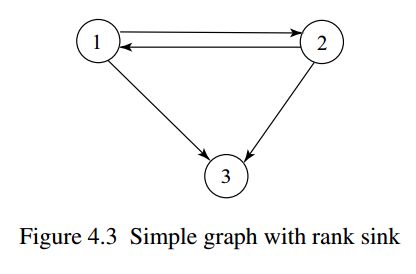
上图中的节点3就是一个dangling node,它只有入边,没有出边,也就是说,每一轮迭代,PR值只会流入3号节点,不会从3号节点流出,久而久之,3就像一个水槽(sink)一样,吸走了大部分的PR,导致PR值虚高。
所以问题随之而来,怎样保证(3)式一定能够收敛到一个平稳概率分布$\pi^T$,$\pi^T$和$\pi^{(0)T}$有关吗,怎样解决dangling nodes问题,等等。此时需要引入一点马尔科夫链理论的知识。
在马尔科夫理论呢中,如果一个矩阵$P$是随机的(stochastic)、不可约的(irreducible)和非周期的(aperiodic),则对于任意的起始向量,都能收敛到一个唯一的平稳正向量。所以如果PageRank矩阵$H$满足上述三个条件,则可以用幂法(Power Method)找到一个平稳概率分布$\pi^T$。幂法是用来计算最大特征值的特征向量。因为$H$的最大特征值为1,所以可以用幂法找到稳态时($\pi^T=\pi^TH$)的概率分布$\pi^T$。
下面我们就将矩阵$H$调整为随机的(stochastic)、不可约的(irreducible)和非周期的(aperiodic)。
行随机矩阵是指行和为1的非负矩阵。如果图中含有dangling nodes,则$H$不是随机的,比如上面的例子,第二行为全0。所以第一个调整是对于所有dangling nodes,都加上一个随机跳转向量$e^T/n$,含义就是如果进入死胡同(dangling nodes),则随机跳转到网络中的任意一个网页。定义向量$a$:
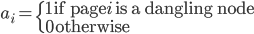
则新的Google矩阵为:
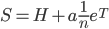
新矩阵$S$就是一个行随机矩阵了。对于上图的例子,有
为了保证矩阵$S$满足不可约性(irreducible)和非周期性(aperiodic),必须使$S$对应的图是强连通的且每个节点有子回路。所以再次调整为:
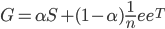
令
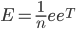
则得到本博客开头的Google矩阵公式:
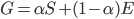
$E$即为随机平均游走矩阵。矩阵$G$也很好解释,大家上网的时候以$\alpha$的概率沿着某个网页里面的链接一步步深入进去($S$),当沿着链接走累的时候,以$1-\alpha$的概率在地址栏输入一个新地址,随机跳走了($E$)。
此时的矩阵$G$满足随机性(stochastic)、不可约性(irreducible)和非周期性(aperiodic),所以可以根据幂法(Power Method)找到一个平稳概率分布$\pi^T$,$\pi^T_i$就衡量了网页$P_i$的重要性或者权威性。
此时只剩下参数$\alpha$了,$\alpha$平衡了网络结构和随机游走。如果$\alpha$很小,则$1-\alpha$大,$G$就退化成一个人造随机网络,不能很好的反应真实的网络结构。如果$\alpha$很大,则有可能不能得到一个稳态分布,或者幂法会失效。当$\alpha\approx 1$时,幂法失效,且$\pi^T(\alpha)$对$H$的微小扰动很敏感。Google的选择是$\alpha=0.85$。
将(5)式带入(6)式,得到
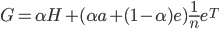
(9)式就非常好计算了,只涉及到向量和矩阵的乘法,而且矩阵$H$还是稀疏矩阵,复杂度还可以降低。
幂法(Power Method)求解PageRank稳态分布就是不断计算下面的等式:
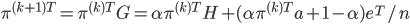
当前后两次的$\pi^{(k+1)T}$和$\pi^{(k)T}$变化小于某个阈值时,算法收敛,所以算法实现是非常容易的。Brin and Page在他们1998年的论文中提到,只需要50-100次迭代运算就可以收敛了。
对于上图的例子,令$\alpha=0.9$,解得
利用幂法解得稳态分布为
所以这6个网页的排名为4>6>5>2>3>1。
真正的搜索引擎应该综合了网页的静态权威性(如PageRank值)和查询的相关性,每个网站都有一个PR值,具体可以点此查询。
本博客主要内容参考Google’s PageRank and Beyond: The Science of Search Engine Rankings[1],插图即为该书封面;如果想快速了解PageRank,可以参考[2];[3]的讲解也很详细。





Pingback: 随机矩阵及其特征值 | bitJoy
写的太好了!!!!!!!!!逻辑清晰,按照文章所述(我没有找到书中的代码[笑cry]),实现了一遍,用文中的小网络做测试,结果完美匹配~!Thanks a lot !
可以看出写得非常认真,希望您的网站的PageRank 也越来越高哦