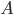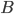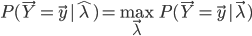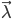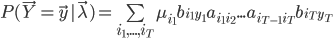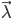随机矩阵是这样一类方阵，其元素为非负实数，且行和或列和为1。如果行和为1，则称为行随机矩阵；如果列和为1，则称为列随机矩阵；如果行和和列和都为1，则称为双随机矩阵。
前面我们介绍的谷歌矩阵和HMM中的转移矩阵都属于随机矩阵，所以随机矩阵也称为概率矩阵、转移矩阵、或马尔可夫矩阵。
随机矩阵有一个性质，就是其所有特征值的绝对值小于等于1，且其最大特征值为1。下面通过两种方法证明这个结论。
首先，随机矩阵A肯定有特征值1，即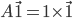
其中的单位向量$\vec 1=(\frac{1}{n},...,\frac{1}{n})^T$，因为A的行和为1，所以上述等式成立。即1是A的特征值。
马尔可夫聚类算法（The Markov Cluster Algorithm, MCL）是一种快速可扩展的基于图的聚类算法。它的基本思想为：在一个稀疏图G中，如果某个区域A是稠密的（是一个聚类），则在A中随机游走k步，还在A内的概率很大，也就是说，A内的k步路径（k-length path）很多。所以我们可以在图中随机游走k步，如果某个区域连通的概率很大，则该区域是一个聚类。随机游走的下一步只和当前所处节点有关，也就是说这是一个马尔可夫的随机游走过程。
我们用一个例子来演示马尔可夫聚类算法的过程。
上一回介绍了HMM的解码问题，今天我们介绍HMM的学习问题和识别问题，先来看学习问题。
正如上一回结束时所说，HMM的学习问题是：仅已知观测序列
，要估计出模型参数组
，其中
为初始概率分布向量，
为转移概率矩阵，
为发射概率矩阵。
算法设计
求解HMM的参数学习问题，就是求解如下的最优化问题：
也就是找一个参数
，使得模型在该参数下最有可能产生当前的观测。如果使用极大似然法求解，对于似然函数
而言，这个最大值问题的计算量过大，在实际中是不可能被采用的。为此，人们构造了一个递推算法，使其能相当合理地给出模型参数的粗略估计。其核心思想是：并不要求备选
使得
达到最大或局部极大，而只要求使相当大，从而使计算变为实际可能。 Continue reading
隐马尔可夫模型（Hidden Markov Model, HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。
先举一个简单的例子以直观地理解HMM的实质——韦小宝的骰子。
半年的时光又过去了，圆满结束了一年的集中教学任务，离开了美丽的雁栖湖，回到闹市中关村。
我们知道常规的快速排序算法是一个不稳定的算法，也就是两个相等的数排序之后的顺序可能和在原序列中的顺序不同。这是因为当选定一个枢轴（pivot），要把其他数分到小于pivot和大于pivot的两边的时候，不同实现的分法不一样。
下面我实现了一种稳定版快速排序算法，在Partition函数中保持了原序列中所有元素的相对顺序，只把pivot放到了它的正确位置。具体方法是三遍扫描原序列：1）第一遍先把小于pivot的元素按先后顺序放到tmp里，然后把pivot放到它的正确位置tmp[k]；2）第二遍把大于pivot的元素按先后顺序追加在tmp里，这样除了pivot以前的其他元素，都保持了和原序列中一样的顺序；3）第三遍把tmp赋值回原数组A。
当排序算法稳定之后，就可以借此统计逆序数了，文件Q5.txt中共包含100000个不同的整数，每行一个数。我们可以使用稳定版快速排序算法对其排序，并统计出其中的逆序数个数。 Continue reading
哈弗曼编码是一个很经典的压缩算法，压缩率能达到50%，甚至更低。它的基本原理包括四个步骤：
解压缩的过程就是解析二进制位，然后查找哈弗曼树，每找到一个叶子节点，就解析出一个字符，直到解析完所有二进制位。下面详细解释我的C++实现。 Continue reading
之前写了七篇博客详细介绍了搜索引擎的工作原理。彼时的搜索引擎主要讲查询和网页的相关性匹配，是动态的、在线的、实时的。相关性匹配有一个问题，网页很容易作弊，比如可以在一个网页中写满诸如“免费”、“美容”之类的垃圾关键词，进而提升查询相关性。但是用户在查询时，一定希望返回的网页比较权威可信，比如同样搜索“苹果电脑”，排名第一的应该是Apple的官网，而不应该是中关村在线之类的第三方网站。
权威性是一个静态的（或者说变化较慢的）衡量网页重要性的指标。但是应该怎样度量权威性呢，HITS算法使用authority来度量，即指向自身的网页数量越多，则自身的authority值越大。谷歌的PageRank算法是用PageRank值来衡量权威性的。HITS和PageRank一个比较大的区别是HITS和查询有关，而PageRank和查询无关，所以PageRank可以离线计算。下面主要介绍PageRank算法。
Continue readingPageRank’s thesis is that a webpage is important if it is pointed to by other important pages.
