原文的第三章内容较多,本博客将分三个部分进行介绍:梯度消失、过拟合与正则化、权重初始化及其他,首先介绍梯度消失问题。
为简单起见,假设网络只包含一个输入和一个神经元,网络的损失是均方误差损失MSE,激活函数是Sigmoid函数。则该网络的参数只包含权重$w$和偏移量$b$。我们想训练这个网络,使得当输入为1时,输出0。

假设我们随机初始化$w_0=0.6$,$b_0=0.9$,则网络的损失随着训练的epoch变化曲线如下,看起来挺好的,一开始损失下降很快,随着epoch增加,损失下降逐渐平缓,直至收敛。

但是,如果随机初始化$w_0=2.0$,$b_0=2.0$,则网络的损失一开始下降得很缓慢,要训练到快200个epoch时,损失才快速下降。可以看到同样是300个epoch,由于初始化权重的差别,损失下降的趋势完全不一样,而且对于下面这种情况,到300个epoch时,损失还有下降的空间,所以期望的output不如上面的接近目标值0。

为什么同样的网络,只是因为初始化权重的差异,损失的变化曲线却相差这么多呢,这和我们选择的损失函数与激活函数有关。
回顾一下,我们在上一讲的末尾介绍到如果损失函数是MSE且激活函数是Sigmoid时,有$\delta^L = (a^L-y) \odot \{\sigma(z^L)(1-\sigma(z^L))\}$,又因为网络只有一个神经元,所以梯度如下:
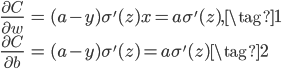
其中第二个等号是把$x=1$和$y=0$带入得到的。由此可见,误差对两个参数$w$和$b$的梯度都和激活函数的导数有关,因为激活函数是Sigmoid,当神经元的输出接近0或1时,梯度几乎为0,误差反向传播就会非常慢,导致上图出现损失下降非常慢的现象。这就是梯度消失的原因。
为了解决这个问题,我们可以采取两种策略,一是替换损失函数,一是替换激活函数。
第一种方法是将MSE的损失函数替换为交叉熵损失函数,激活函数依然是Sigmoid。我们考虑一个比本文开头更复杂的网络,仍然是一个输出神经元,但包含多个输入神经元。

此时,交叉熵损失函数定义如下,其中的$n$表示训练样本数,$\frac{1}{n}\sum_x$表示对所有输入样本$x$的交叉熵损失求均值。
![\begin{eqnarray}C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right]\tag{3}\end{eqnarray}](https://bitjoy.net/wp-content/plugins/latex/cache/tex_bb787f080fd5d4f3fc61f2c2fe886f60.gif)
我们首先考察为什么(3)可以是一个损失函数,损失函数需要满足如下两个条件:
- 非负;
- 当网络输出和目标答案越接近,损失越小;反之损失越大。
简单代入几组不同的样本很容易验证交叉熵满足上述两个条件 ,所以交叉熵可以作为一个损失函数。
下面我们再考察一下为什么交叉熵损失函数+Sigmoid激活函数可以解决梯度消失的问题。首先推导交叉熵损失$C$对权重$w_j$和$b$的梯度:

上式分子Sigmoid的导数正好可以和分母抵消,得到:
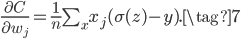
类似的,可得:
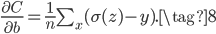
非常神奇的,我们发现交叉熵损失函数对参数的梯度中不存在Sigmoid的导数了!这样就不受Sigmoid两端梯度消失的影响了!而且从(7)和(8)还可以发现,当网络的输出$\sigma(z)$和目标结果$y$差距越大,梯度越大;差距越小,梯度越小。这和人类的学习过程很相似,当犯错越大,教训越大,得到的经验也越多,提升也越明显。
换成交叉熵损失函数+Sigmoid激活函数的组合后,我们再看看之前的两个例子:


和预期的结果一样,无论哪一种情况,由于刚开始时网络的输出和预期答案差距较大,所以梯度也大,损失下降也很快,不再出现梯度消失的问题了。
上面的讨论是基于输出层只有一个神经元的情况,如果输出层有$j$个神经元,交叉熵公式如下,结论是一样的。
![\begin{eqnarray} C = -\frac{1}{n} \sum_x\sum_j \left[y_j \ln a^L_j + (1-y_j) \ln (1-a^L_j) \right].\tag{9}\end{eqnarray}](https://bitjoy.net/wp-content/plugins/latex/cache/tex_fb8c44262c2374f889ea72d385ad7af3.gif)
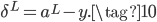
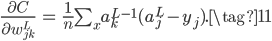
如果输出层神经元的激活函数都是线性的,不再是Sigmoid函数,此时依然使用MSE损失函数也没有梯度消失的问题,公式如下:
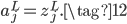
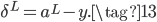

那么交叉熵这个损失函数是怎么来的呢,是碰巧有人发现使用交叉熵能抵消Sigmoid的梯度消失问题吗?事实上,我们可以从MSE+Sigmoid的梯度消失问题中推导得到交叉熵损失函数。还是以开头只有一个神经元的网络为例,对于公式(1)和(2),如果希望能抵消掉激活函数的导数$\sigma'(z)$,则我们的目标为:
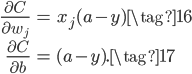
又根据原始推导和Sigmoid导数有:
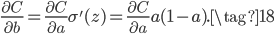
对比公式(17)有:
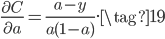
据此可推导得到损失函数为:
![\begin{eqnarray}C = -[y \ln a + (1-y) \ln (1-a)]+ {\rm constant},\tag{20}\end{eqnarray}](https://bitjoy.net/wp-content/plugins/latex/cache/tex_9f7f59c15b08fe8824fd3a601ef5bb4d.gif)
如果有多个输入样本,则损失函数为:
![\begin{eqnarray}C = -\frac{1}{n} \sum_x [y \ln a +(1-y) \ln(1-a)] + {\rm constant},\tag{21}\end{eqnarray}](https://bitjoy.net/wp-content/plugins/latex/cache/tex_1def619307d3070fd64c34a1decae726.gif)
可以看到,上式本质上和公式(3)是一样的,这就是交叉熵损失函数!所以交叉熵并不神秘,不是拍脑袋凭空想出来的,而是可以根据目标求解出来的一个损失函数。
上面介绍了第一种替换损失函数但保留Sigmoid激活函数来解决梯度消失的方法,第二种方法就是把损失函数和激活函数都换掉的方法,损失函数替换为log似然损失,激活函数替换为Softmax。
Softmax激活函数的公式如下:
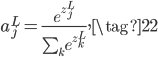
此时,某个神经元的输出$a_j^L$不再只跟它自己未激活的$z_j^L$有关,而是和所有的未激活值$z_k^L$有关。而且$a_j^L$有一个很好的特性,它用所有未激活值的和做了归一化,所以每个输出$a_j^L$可以看成输出为$j$的概率值,满足:
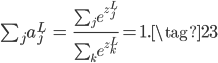
log似然损失函数如下:
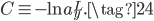
比如在手写数字识别问题中,如果输入是一个$7$的图片,那么对应这个样本的损失就是$-\ln a^L_7$,如果输出的第7个神经元的概率$a_7^L$很高接近于1,则损失$-\ln a^L_7$会很小;反之,如果$a_7^L$很低接近于0,则损失$-\ln a^L_7$会很大。
同样的,我们可以推导得到试用log似然损失+Softmax也能解决梯度消失的问题,对应的梯度如下,和公式(14)和(15)是一样的。
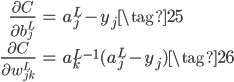
事实上,Softmax相当于Sigmoid在多元情况下的推广,交叉熵损失(9)的每一项也就是log似然损失(24)。回顾逻辑回归那篇博客,有非常多的相似点。
最后总结,对于一个神经网络,判断是否有梯度消失的问题,最根本的方法就是求解损失对参数的梯度,如果梯度中包含可能出现梯度消失的项,则存在梯度消失的问题,否则不存在。而梯度求解又和所选的损失函数和激活函数有关,目前比较好的组合是MSE+线性激活、交叉熵+Sigmoid、log似然+Softmax,这几种组合都不会有梯度消失的问题。
Pingback: CS224N(1.29)Vanishing Gradients, Fancy RNNs | bitJoy
Pingback: Neural Networks and Deep Learning(五)为什么深度神经网络难以训练 | bitJoy